2015年高考数学新课标II卷(理科)压轴题(第21题):
设函数\(f(x)={\rm e}^{mx}+x^2-mx\).
(1)证明:\(f(x)\)在\((-\infty,0)\)单调递减,在\((0,+\infty)\)单调递增;
(2)若对于任意\(x_1,x_2\in [-1,1]\),都有\(\left|f\left(x_1\right)-f\left(x_2\right)\right|\leqslant {\rm e}-1\),求\(m\)的取值范围.
(1)证明 根据题意\[f'(x)=m{\rm e}^{mx}+2x-m,\]注意到\(f'(0)=0\),于是再求导\[f'^\prime (x)=m^2{\rm e}^{mx}+2,\]由于\(f'^\prime (x)>0\),于是\(y=f'(x)\)为单调递增函数,结合\(f'(0)=0\),有\(f'(x)\)在\((-\infty,0)\)上恒小于\(0\),在\((0,+\infty)\)上恒大于\(0\).因此原命题得证.
(2)解 根据题意,函数\(f(x)\)在区间\([-1,1]\)上的最大值与最小值之差不超过\({\rm e}-1\).由第1小题可知\(f(x)\)在区间\([-1,1]\)上的最小值为\(f(0)=1\),于是问题转化为\(f(x)\)在区间\([-1,1]\)上的最大值不超过\({\rm e}\).
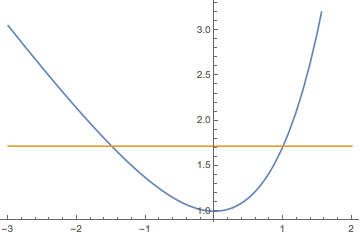
根据第1小题,函数\(f(x)\)在区间\([-1,1]\)上的最大值为\(f(1)\)和\(f(-1)\)中较大者,因此\(m\)的取值范围由\[\begin{cases}f(-1)\leqslant {\rm e},\\f(1)\leqslant {\rm e},\end{cases}\]确定,即\[\begin{cases}{\rm e}^{-m}+1+m\leqslant {\rm e},\\{\rm e}^{m}+1-m\leqslant {\rm e},\end{cases}\]变形得\[\begin{cases}{\rm e}^m-m\leqslant {\rm e}-1,\\{\rm e}^{-m}+m\leqslant {\rm e}-1,\end{cases}\]记函数\(g(x)={\rm e}^x-x\),则\[g'(x)={\rm e}^x-1,\]于是\(g(x)\)在\(x<0\)时单调递减,在\(x>0\)时单调递增,如图.
因此不难解得\(m\)的取值范围为\([-1,1]\).