(理8)已知函数$$f(x)=\begin{cases}x^2-x+3,&x\leqslant 1,\\ x+\dfrac 2x,&x>1,\end{cases}$$设$a\in \mathbb R$，若关于$x$的不等式$f(x)\geqslant \left|\dfrac x2+a\right|$在$\mathbb R$上恒成立，则$a$的取值范围是( )
A．$\left[-\dfrac{47}{16},2\right]$
B．$\left[-\dfrac{47}{16},\dfrac{39}{16}\right]$
C．$\left[-2\sqrt 3,2\right]$
D．$\left[-2\sqrt 3,\dfrac{39}{16}\right]$
分析与解 A．
根据题意，有\[\forall x\in\mathbb R,-f(x)-\dfrac x2\leqslant a\leqslant f(x)-\dfrac x2,\]因此只需要计算函数$g(x)=-f(x)-\dfrac x2$在$\mathbb R$上的最大值和函数$h(x)=f(x)-\dfrac x2$在$\mathbb R$上的最小值即可．函数$g(x)$即\[g(x)=\begin{cases}-x^2+\dfrac x2-3,&x\leqslant 1,\\ -\dfrac 32x-\dfrac 2x,& x>1,\end{cases}\]其最大值为\[\max\{g(x)\}=\max\left\{-\dfrac{47}{16},-2\sqrt{3}\right\}=-\dfrac{47}{16}.\]函数$h(x)$即\[h(x)=\begin{cases} x^2-\dfrac 32x+3,&x\leqslant 1,\\ \dfrac x2+\dfrac 2x,& x>1,\end{cases}\]其最小值为\[\min\{h(x)\}=\min\left\{\dfrac{39}{16},2\right\}=2.\]因此所求的取值范围是$\left[-\dfrac{47}{16},2\right]$．
(理14)用数字$1,2,3,4,5,6,7,8,9$组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有______个．(用数字作答)
分析与解 $1080$．
情形一 四位数中没有偶数数字，个数为\[{\rm A}_5^4=120.\]
情形二 四位数中有一个偶数数字，个数为\[{\rm C}_4^1{\rm C}_5^3{\rm A}_4^4=960.\]
因此符合题意的四位数共有$120+960=1080$个．
(理19)设椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的左焦点为$F$，右顶点为$A$，离心率为$\dfrac 12$．已知$A$是抛物线$y^2=2px$($p>0$)的焦点，$F$到抛物线的准线$l$的距离为$\dfrac 12$．
(1)求椭圆的方程和抛物线的方程；
(2) 设$l$上两点$P,Q$关于$x$轴对称，直线$AP$与椭圆相交于点$B$($B$异于点$A$)，直线$BQ$与$x$轴相交于点$D$，若$\triangle APD$的面积为$\dfrac{\sqrt 6}2$，求直线$AP$的方程．
分析与解 (1) 根据题意，抛物线的准线$l$过椭圆的左顶点，因此有\[\begin{cases}\dfrac ca=\dfrac 12,\\ a-c=\dfrac 12,\end{cases}\]其中$c$为椭圆的半焦距．解方程，可得椭圆的方程为$$x^2+\dfrac{4y^2}3=1,$$抛物线的方程为$$y^2=4x.$$
(2) 如图．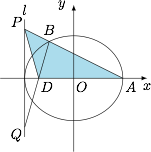
考虑到图形的对称性，先计算$B$点纵坐标为正实数的情形．设$B\left(\cos\theta,\dfrac{\sqrt 3}2\sin \theta\right)$，$P(-1,m)$，则\[\dfrac{m-0}{-1-1}=\dfrac{\dfrac{\sqrt 3}2\sin\theta-0}{\cos\theta-1},\]解得\[m=\dfrac{\sqrt{3}\sin\theta}{1-\cos\theta}.\]于是$Q\left(-1,\dfrac{\sqrt 3\sin\theta}{\cos\theta-1}\right)$，进而可得$D$点的横坐标为\[\dfrac{\cos\theta\cdot \dfrac{\sqrt 3\sin\theta}{\cos\theta-1}-(-1)\cdot\dfrac{\sqrt 3}2\sin\theta}{\dfrac{\sqrt 3\sin\theta}{\cos\theta-1}-\dfrac{\sqrt 3}2\sin\theta}=\dfrac{3\cos\theta-1}{3-\cos\theta}.\]这样得到$\triangle APD$的面积\[\begin{split} S=&\dfrac 12\cdot \left(1-\dfrac{3\cos\theta-1}{3-\cos\theta}\right)\cdot \dfrac{\sqrt 3\sin\theta}{1-\cos\theta}\\=&\dfrac{2\sqrt3\sin\theta}{3-\cos\theta}=\dfrac{\sqrt 6}2,\end{split} \]解得$\cos\theta=\dfrac 13$，$\sin\theta=\dfrac{2\sqrt 2}3$．进而可得直线$AP$的方程为\[y=-\dfrac{\sqrt 6}2x+\dfrac{\sqrt 6}2.\]
结合图形的对称性，可得直线$AP$的方程为$y=-\dfrac{\sqrt 6}2x+\dfrac{\sqrt 6}2$或$y=\dfrac{\sqrt 6}2x-\dfrac{\sqrt 6}2$．
(理20)设$a\in\mathbb Z$，已知定义在$\mathbb R$上的函数$f(x)=2x^4+3x^3-3x^2-6x+a$在区间$(1,2)$内有一个零点$x_0$，$g(x)$为函数$f(x)$的导函数．
(1) 求$g(x)$的单调区间；
(2) 设$m\in [1,x_0)\cup (x_0,2]$，函数$h(x)=g(x)(m-x_0)-f(m)$，求证：$h(m)h(x_0)<0$；
(3) 求证：存在大于$0$的常数$A$，使得对于任意的正整数$p,q$，且$\dfrac pq\in [1,x_0)\cup (x_0,2]$，满足$\left|\dfrac pq-x_0\right|\geqslant \dfrac{1}{Aq^4}$．
分析与解 (1) 函数$g(x)$为\[g(x)=8x^3+9x^2-6x-6,\]其导函数为\[g'(x)=24x^2+18x-6=6(4x-1)(x+1),\]因此函数$g(x)$的单调递增区间为$(-\infty,-1)$和$\left(\dfrac 14,+\infty\right)$；单调递减区间为$\left(-1,\dfrac 14\right)$．
(2) 令$\varphi(x)=g(x)(x-x_0)-f(x)$，则其导函数\[\varphi'(x)=g'(x)(x-x_0),\]而在$[1,2]$上，$g'(x)>0$，因此$\varphi(x)$在$[1,x_0)$上单调递减，在$(x_0,2]$上单调递增，进而在$[1,x_0)\cup (x_0,2]$上，$\varphi(x)>0$，故\[h(m)=\varphi(m)>0.\]
令$\mu(x)=g(x_0)(x-x_0)-f(x)$，则其导函数\[\mu'(x)=g(x_0)-g(x),\]而在$[1,2]$上，$g(x)$单调递增，因此$\mu(x)$在$[1,x_0)$上单调递增，在$(x_0,2]$上单调递减，进而在$[1,x_0)\cup (x_0,2]$上，$\mu(x)<0$，故\[h(x_0)=\mu(m)<0.\]
综上所述，有$h(m)\cdot h(x_0)<0$，命题得证．
(3) 由于函数$h(x)$在$[1,2]$上单调，根据第(2)小题$h(x)$在$m$和$x_0$之间存在唯一零点．令$m=\dfrac pq$，$h(x)$在$m$和$x_0$之间的零点为$x_1$，则有\[h(x_1)=g(x_1)\left(\dfrac pq-x_0\right)-f\left(\dfrac pq\right)=0,\]进而\[\left|\dfrac pq-x_0\right|=\dfrac{\left|f\left(\dfrac pq\right)\right|}{g(x_1)}=\dfrac{\left|2p^4+3p^3q-3p^2q^2-6pq^3+aq^4\right|}{g(x_1)\cdot q^4},\]由于$\dfrac pq\ne x_0$，而函数$f(x)$在$[1,2]$内的零点唯一，因此$$\left|2p^4+3p^3q-3p^2q^2-6pq^3+aq^4\right|\ne 0,$$进而有\[\left|2p^4+3p^3q-3p^2q^2-6pq^3+aq^4\right|\geqslant 1,\]又因为$g(x)$在$[1,2]$上单调递增，所以$$g(x_1)\in[g(1),g(2)]=[5,82],$$因此取$A=82$即可，因此命题得证．