(理8)根据有关资料，围棋状态空间复杂度的上限$M$约为$3^{361}$，而可观测宇宙中普通物质的原子总数$N$约为$10^{80}$，则下列各数中与$\dfrac{M}{N}$最接近的是( )(参考数据$\lg 3\approx 0.48$)
A．$10^{33}$
B．$10^{53}$
C．$10^{73}$
D．$10^{93}$
分析与解 D．
考虑到\[M\approx 3^{361}=10^{361\lg 3}\approx 10^{173.28} \approx N\cdot 10^{93.28},\]因此选项D符合题意．
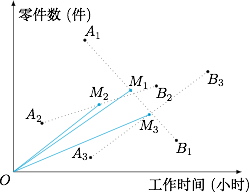
(理14)三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中点$A_i$的横、纵坐标分别为第$i$名工人上午的工作时间和加工的零件数，点$B_i$的横、纵坐标分别为第$i$名工人下午的工作时间和加工的零件数，$i=1,2,3$．
(1) 记$Q_i$为第$i$名工人在这一天加工的零件总数，则$Q_1,Q_2,Q_3$中最大的是_______；
(2) 记$p_i$为第$i$名工人在这一天中平均每小时加工的零件数，则$p_1,p_2,p_3$中最大的是_______．
分析与解 (1)$Q_1$；(2)$p_2$．
(1)比较线段$A_iB_i$的中点$M_i$的纵坐标大小即可；
(2)比较直线$OM_i$的斜率大小即可．
(理18)已知抛物线$C:y^2=2px$过点$P(1,1)$，过点$\left(0,\dfrac 12\right)$作直线$l$与抛物线$C$交于不同的两点$M,N$．过点$M$作$x$轴的垂线分别与直线$OP,ON$交于点$A,B$，其中$O$为原点．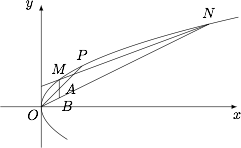
(1) 求抛物线$C$的方程，并求其焦点坐标和准线方程；
(2) 求证：$A$为线段$BM$的中点．
分析与解 (1) 根据题意可得$p=\dfrac 12$，于是抛物线$C$的方程为$y^2=x$，焦点坐标为$\left(\dfrac 14,0\right)$，准线方程为$x=-\dfrac14$．
(2) 设$M(m^2,m)$，$N(n^2,n)$，则\[\dfrac{m^2\cdot n-n^2\cdot m}{m^2-n^2}=\dfrac 12,\]即\[\dfrac 1m+\dfrac 1n=2.\]此时$A\left(m^2,m^2\right)$，$B\left(m^2,\dfrac{m^2}{n}\right)$，因此$A$为线段$BM$的中点即\[m+\dfrac{m^2}{n}=2m^2,\]这显然成立，原命题得证．
(理19)已知函数$f(x)={\rm e}^x\cos x-x$．
(1) 求曲线$y=f(x)$在点$(0,f(0))$处的切线方程；
(2) 求函数$f(x)$在区间$\left[0,\dfrac{\pi}2\right]$上的最大值和最小值．
分析与解 (1) 函数$f(x)$的导函数$$f'(x)={\rm e}^x(\cos x-\sin x)-1,$$于是所求的切线方程为\[y=f'(0)x+f(0),\]即$y=1$．
(2) 函数$f'(x)$的导函数$$f''(x)=-2{\rm e}^x\sin x,$$于是在区间$\left[0,\dfrac{\pi}2\right]$上，$f''(x)\leqslant 0$，$f'(x)$单调递减；又$f'(0)=0$，于是$f'(x)\leqslant 0$，$f(x)$单调递减．因此函数$f(x)$在区间$\left[0,\dfrac{\pi}2\right]$的最大值为$f(0)=1$，最小值为$f\left(\dfrac{\pi}2\right)=-\dfrac{\pi}2$．
(题20)设$\{a_n\}$和$\{b_n\}$是两个等差数列，记\[c_n=\max\{b_1-a_1n,b_2-a_2n,\cdots,b_n-a_nn\},\]其中$n=1,2,3,\cdots$，$\max\{x_1,x_2,\cdots,x_s\}$表示$x_1,x_2,\cdots,x_s$这$s$个数中最大的数．
(1) 若$a_n=n$，$b_n=2n-1$，求$c_1,c_2,c_3$的值，并证明$\{c_n\}$是等差数列；
(2) 证明：或者对任意正数$M$，存在正整数$m$，当$n\geqslant m$时，$\dfrac{c_n}{n}>M$；或者存在正整数$m$，使得$$c_m,c_{m+1},c_{m+2},\cdots$$是等差数列．
分析与解 (1) 根据定义，有\[\begin{split}
c_1&=b_1-a_1=0,\\c_2&=\max\{b_1-2a_1,b_2-2a_2\}=\max\{-1,-1\}=-1,\\c_3&=\max\{b_1-3a_1,b_2-3a_2,b_3-3a_3\}=\max\{-2,-3,-4\}=-2.\end{split}\]事实上，设$x_k=2k-1-kn$，则有\[c_n=\max\{x_1,x_2,\cdots,x_n\},\]当$n\geqslant 2$，且$k=2,3,\cdots,n$时，有\[x_k-x_{k-1}=2-n\leqslant 0,\]于是\[c_n=x_1=1-n,\]结合$c_1=0$，因此数列$\{c_n\}$是等差数列．
(2) 不妨设$a_n=a_0+nd_1$，$b_n=b_0+nd_2$，其中$n\in \mathbb N^*$．考虑\[x_k=b_0+kd_2-(a_0+kd_1)n=(b_0-a_0n)+(d_2-d_1n)k,\]这是关于$k$的等差数列，因此\[c_n=\max\{c_1,c_n\}=\max\{b_1-a_1n,b_0+(d_2-a_0)n-d_1n^2\}.\]考虑函数$f(x)=b_1-a_1x$和函数$g(x)=b_0+(d_2-a_0)x-d_1x^2$，分类讨论如下．
情形一 $d_1\ne 0$．此时$f(x)$的图象是直线，$g(x)$的图象是抛物线，无论直线与抛物线的位置关系如何，必然存在正整数$m_0$，使得\[\forall x\geqslant m_0,\max\{f(x),g(x)\}=f(x),\]或\[\forall x\geqslant m_0,\max\{f(x),g(x)\}=g(x).\]当$\forall x\geqslant m_0,\max\{f(x),g(x)\}=f(x)$时，取$m=m_0$，有$$c_m,c_{m+1},c_{m+2},\cdots$$是等差数列；而当$\forall x\geqslant m_0,\max\{f(x),g(x)\}=g(x)$时，必然有$g(x)$开口向上，即$-d_1>0$，因此\[\dfrac{g(x)}x=\dfrac{b_0}x-d_1x+(d_2-a_0),\]对任意正数$M$，必然存在正整数$m_1$，使得当$x\geqslant m_1$时，有\[\dfrac{g(x)}{x}>M,\]此时取$m=\max\{m_0,m_1\}$，可得当$n\geqslant m$时，$\dfrac{c_n}{n}>M$．
情形二 $d_1=0$．此时$f(x)$与$g(x)$的图象都是直线，无论这两条直线位置关系如何，必然存在正整数$m$，使得\[\forall x\geqslant m,\max\{f(x),g(x)\}=f(x),\]或\[\forall x\geqslant m,\max\{f(x),g(x)\}=g(x),\]这就意味着$$c_m,c_{m+1},c_{m+2},\cdots$$是等差数列．
综上所述，原命题得证．