2017年高考浙江卷理科压轴题详解

(题10)如图，已知平面四边形$ABCD$，$AB\perp BC$，$AB=BC=AD=2$，$CD=3$．$AC$与$BD$交于点$O$，记$I_1=\overrightarrow{OA}\cdot \overrightarrow{OB}$，$I_2=\overrightarrow{OB}\cdot \overrightarrow{OC}$，$I_3=\overrightarrow{OC}\cdot \overrightarrow{OD}$，则(　　)

A．$I_1<I_2<I_3$
B．$I_1<I_3<I_2$
C．$I_3<I_1<I_2$
D．$I_2<I_1<I_3$

---

分析与解　C．

如图，作线段$AC$的垂直平分线$l$．

由于$DA<DC$，因此$A,D$在直线$l$同侧，进而$OA<OC$，$\angle ABO<45^\circ$，进而 $$\angle AOD=\angle ABO+\angle BAO<90^\circ,$$ 在等腰三角形$ABD$中，$OB<OD$．这样就有 $$I_3=|OC|\cdot |OD|\cdot \cos\angle COD<|OA|\cdot |OB|\cdot \cos\angle AOB=I_1<0<I_2.$$

---

(题17)已知$a\in\mathbb R$，函数$f(x)=\left|x+\dfrac 4x-a\right|+a$在区间$[1,4]$上的最大值是$5$，则$a$的取值范围是______．

分析与解　$\left(-\infty,\dfrac 92\right]$．

考虑到 $$f(x)=\left|g(x)-a\right|+a$$ 即 $$f(x)=\begin{cases} 2a-g(x),& g(x)<a,\\ g(x),& g(x)>a,\end{cases}$$ 其几何意义为将函数$g(x)$的图象在直线$y=a$下方的部分翻折到直线$y=a$上方．结合函数$g(x)=x+\dfrac 4x$在$[1,4]$上的图象，可得$a$的取值范围是$\left(-\infty,\dfrac 92\right]$．

---

(理21)如图，已知抛物线$x^2=y$，点$A\left(-\dfrac 12,\dfrac 14\right)$，$B\left(\dfrac 32,\dfrac 94\right)$，抛物线上的点$P(x,y)$($-\dfrac 12<x<\dfrac 32$)．过点$B$作直线$AP$的垂线，垂足为$Q$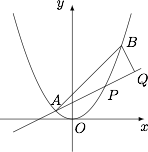．(1) 求直线$AP$斜率的取值范围；

(2) 求$|PA|\cdot |PQ|$的最大值．

分析与解　(1) 直线$AP$的斜率 $$k=\dfrac{x^2-\dfrac 14}{x-\left(-\dfrac 12\right)}=x-\dfrac 12,$$ 取值范围为$(-1,1)$．

(2) 根据题意，有 $$\begin{split}|PA|\cdot |PQ|&=-\overrightarrow{PA}\cdot \overrightarrow{PQ}\\&=-\overrightarrow{PA}\cdot \overrightarrow{PB}\\&=\left(x+\dfrac 12\right)\left(\dfrac 32-x\right)+\left(x^2-\dfrac 14\right)\left(\dfrac 94-x^2\right)\\&=\left(x+\dfrac 12\right)\left(\dfrac 32-x\right)\left[1+\left(x-\dfrac 12\right)\left(\dfrac 32+x\right)\right]\\&=\left(x+\dfrac 12\right)^3\left(\dfrac 32-x\right)\\&=\dfrac 13\left(x+\dfrac 12\right)\left(x+\dfrac 12\right)\left(x+\dfrac 12\right)\left(\dfrac 92-3x\right)\\&\leqslant \dfrac 13\left(\dfrac {3x+\dfrac 32+\dfrac 92-3x}{4}\right)^4\\&=\dfrac{27}{16},\end{split}$$ 等号当且仅当$x=1$时取得．因此所求的最大值为$\dfrac{27}{16}$．

---

(理22)已知数列$\{x_n\}$满足：$x_1=1$，$x_n=x_{n+1}+\ln (1+x_{n+1})$($n\in\mathbb N^*$)．证明：当$n\in\mathbb N^*$时，

(1) $0<x_{n+1}<x_n$；

(2) $2x_{n+1}-x_n\leqslant \dfrac{x_nx_{n+1}}2$；

(3) $\dfrac{1}{2^{n-1}}\leqslant x_n\leqslant \dfrac{1}{2^{n-2}}$．

分析与解　(1) 先证明$x_n>0,n\in\mathbb N^*$，用数学归纳法．当$n=1$时，命题显然成立．设当$n=k$，$k\in\mathbb N^*$时命题成立，即$x_k>0$，则考虑到函数 $$f(x)=x+\ln(1+x)$$ 是单调递增函数，且有$f(0)=0,x_n=f(x_{n+1})$，所以 $$f(0)<x_k=f(x_{k+1})<x_k+\ln(1+x_k)=f(x_k),$$ 由单调性知$0<x_{k+1}<x_k$，因此命题对$n=k+1$也成立，且$0<x_{n+1}<f(x_{n+1})=x_n$．

 

(2) 即证明 $$x_n\geqslant \dfrac{2x_{n+1}}{1+\dfrac 12x_{n+1}},$$ 也即 $$x_{n+1}+\ln (1+x_{n+1})\geqslant \dfrac{4x_{n+1}}{2+x_{n+1}},$$ 等价于 $$\ln(1+x_{n+1})\geqslant \dfrac{2x_{n+1}-x_{n+1}^2}{2+x_{n+1}}.$$ 我们熟知当$x>0$时，有 $$\ln(1+x)>\dfrac{2x}{2+x},$$ 因此 $$\ln(1+x_{n+1})>\dfrac{2x_{n+1}}{2+x_{n+1}}>\dfrac{2x_{n+1}-x_{n+1}^2}{2+x_{n+1}},$$ 原命题得证．

(3) 我们熟知$\ln x\leqslant x-1$，因此有 $$x_n=x_{n+1}+\ln(1+x_{n+1})\leqslant 2x_{n+1},$$ 于是 $$\dfrac{x_{n+1}}{x_n}\geqslant \dfrac 12,$$ 这样就有 $$\dfrac{x_n}{x_1}=\prod_{k=1}^{n-1}\dfrac{x_{k+1}}{x_k}\geqslant \left(\dfrac 12\right)^{n-1},$$ 左边不等式成立．

根据第(2)小题结论，我们有 $$\dfrac{2}{x_n}-\dfrac{1}{x_{n+1}}\leqslant \dfrac 12,$$ 考虑不动点，有 $$\dfrac{\dfrac{1}{x_{n+1}}-\dfrac 12}{\dfrac 1{x_n}-\dfrac 12}\geqslant 2,$$ 因此可得 $$\dfrac{1}{x_n}-\dfrac 12\geqslant 2^{n-2},$$ 从而 $$x_n\leqslant \dfrac{1}{2^{n-2}+\dfrac 12}\leqslant \dfrac{1}{2^{n-2}},$$ 右边不等式成立．

综上所述，原命题得证．