已知$\triangle ABC$中，$A:B:C=1:3:9$，求$\cos A+\cos B+\cos C$．
分析与解 易知$A=\dfrac{\pi}{13}$，$B=\dfrac{3\pi}{13}$，$C=\dfrac{9\pi}{13}$，记$x_k=\cos\dfrac{k\pi}{13}$，其中$k\in\mathcal N$．
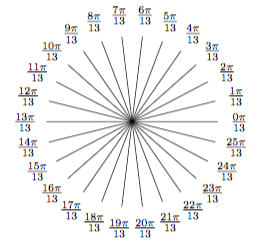所求代数式$m=x_1+x_3+x_9$，有\[\begin{split} m^2
&=x_1^2+x_3^2+x_9^2+2x_1x_3+2x_3x_9+2x_9x_1\\
&=\dfrac{1+x_2}{2}+\dfrac{1+x_6}{2}+\dfrac{1+x_{18}}{2}+x_4+x_2+x_{12}+x_6+x_{10}+x_8\\
&=x_2+x_4+x_6+x_8+x_{10}+x_{12}+\dfrac 12x_2+\dfrac 12x_6+\dfrac 12x_8+\dfrac 32
,\end{split} \]
又$$m=x_1+x_3+x_9=-x_{12}-x_{10}-x_4,$$从而\[\begin{split} m^2-\dfrac 12m&=\dfrac 32+\dfrac 32\left(x_2+x_4+x_6+x_8+x_{10}+x_{12}\right)\\
&=\dfrac 32+\dfrac 34\left(x_2+x_4+\cdots +\cdots +x_{24}+x_0\right)-\dfrac 34x_0\\
&=\dfrac 32-\dfrac 34=\dfrac 34,\end{split} \]
从而$$4m^2-2m-3=0,$$解得$m=\dfrac{1+\sqrt{13}}4$(负号舍去)．
注 上面用到了结论$$\cos\dfrac{0}{2k+1}+\cos\dfrac{2\pi}{2k+1}+\cos\dfrac{4\pi}{2k+1}+\cdots+\cos\dfrac{4k\pi}{2k+1}=0.$$可以将左边乘以$\sin\dfrac{2\pi}{2k+1}$，再积化和差去证明，也可以设$\omega=\cos\dfrac{2\pi}{2k+1}+{\rm i}\sin\dfrac{2\pi}{2k+1}$，通过计算$\omega+\omega^2+\cdots+\omega^{2k}$得到结果．