在有理数范围内分解因式：$x^{12}+x^9+x^6+x^3+1$．
分析与解 等比数列求和可得\[\begin{split} x^{12}+x^9+x^6+x^3+1&=\dfrac{x^{15}-1}{x^3-1}\\ &=\dfrac{x^5-1}{x-1}\cdot \dfrac{x^{10}+x^5+1}{x^2+x+1}\\ &=(x^4+x^3+x^2+1)(x^8-x^7+x^5-x^4+x^3-x+1).\end{split} \]方程$x^{{12}}+x^{9}+x^{6}+x^{3}+1=0$的所有复数根分布如下图．
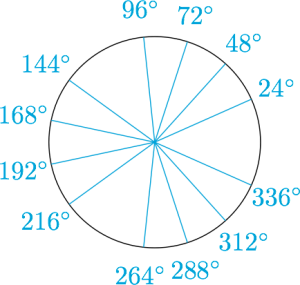我们熟知，如果$\cos\theta$是有理数，则$\cos n\theta$亦为有理数，其中$n\in\mathcal N^*$，因此若$\cos n\theta$不是有理数，那么$\cos\theta$也不是有理数，因此可以按照以下路径推出图中所有角的余弦均不为有理数($\cos 144^\circ=-\dfrac{\sqrt 5+1}4$)：$$144^\circ\to 72^\circ \to 24^\circ\to 336^\circ\to 168^\circ\to 192^\circ\to 96^\circ\to 48^\circ.$$由于任何共轭的复数根其实部均不为有理数，所以无法在有理数范围内继续分解因式．
综上，题中代数式分解因式的结果为$(x^4+x^3+x^2+1)(x^8-x^7+x^5-x^4+x^3-x+1)$．
说明 下面说明如何计算$\cos 36^\circ$：
1．$\cos 36^{\circ}\cdot\cos 72^{\circ}=\dfrac{\sin 36^\circ\cdot\cos 36^{\circ}\cdot\cos 72^\circ}{\sin 36^\circ}=\dfrac 14$；
2．因为$\cos 72^\circ=2\cos^2 36^\circ-1$，所以$\cos 36^\circ$满足方程$x(2x^2-1)=\dfrac 14$，对此方程整理变形得$$(2x+1)(4x^2-2x-1)=0,$$所以$\cos 36^\circ=\dfrac {1+\sqrt 5}{2}$．
3．也可以由$\cos 36^\circ-\cos 72^\circ=2\sin 54^\circ\sin 18 ^\circ=2\cos 72^\circ\cos 36^\circ=\dfrac 12$，得到$\cos 36^\circ$与$-\cos 72^\circ$是方程$x^2-\dfrac 12x-\dfrac 14=0$的两根，从而有$$\cos 36^\circ=\dfrac {1+\sqrt 5}{4},\cos 72^\circ=\dfrac {\sqrt 5-1}{4}.$$