处理极值点偏移问题的三驾马车

已知$f(x)=x\ln x-\dfrac{k}{x}$的两个零点为$x_1,x_2$，记$f(x)$的导函数为$f'(x)$，求证：$f'\left(\dfrac{x_1+x_2}2\right)\neq 0$．

分析　这是包含对数函数的极值点偏移问题，可以考虑用齐次化，对称化以及构造函数．

齐次化方法　根据已知，有$x_1^2\ln x_1=x_2^2\ln x_2=k$，设$\dfrac{x_1}{x_2}=t$，$t>1$，则 $$x_1^2=\dfrac{k(1-t^2)}{\ln t},x_2^2=\dfrac{k(1-t^2)}{t^2\ln t},k<0.$$ 由于$f'(x)=1+\ln x+\dfrac{k}{x^2}$，于是 $$f'\left(\dfrac{x_1+x_2}2\right)=1+\ln\dfrac{x_1+x_2}2+\dfrac{k}{\left(\dfrac{x_1+x_2}2\right)^2}>1+\ln\dfrac{(t+1)x_2}2+\dfrac{k}{x_1x_2},$$ 将$x_1^2,x_2^2$代入(其中$\ln x_2=\dfrac{k}{x_2^2}$)，得 $$f'\left(\dfrac{x_1+x_2}2\right)>1+\ln\dfrac{t+1}2+\dfrac{t^2\ln t}{1-t^2}-\dfrac{t\ln t}{t^2-1}=1+\ln\dfrac{t+1}2+\dfrac{t\ln t}{1-t}.$$ 接下来用分析法证明 $$\forall t>1,1+\ln\dfrac{t+1}2+\dfrac{t\ln t}{1-t}>0,$$ 即 $$\forall t>1,t-1+(t-1)\ln\dfrac{t+1}2-t\ln t>0.$$ 设$\varphi(t)=t-1+(t-1)\ln\dfrac{t+1}2-t\ln t$($t>1$)，则其导函数 $$\varphi'(t)=\dfrac{t-1}{t+1}+\ln\dfrac{t+1}{2t}>\dfrac{t-1}{t+1}+\left(1-\dfrac{2t}{t+1}\right)=0,$$ 其中用到了不等式$\ln x\geqslant 1-\dfrac 1x$(等号当且仅当$x=1$时取得)．因此$\varphi(t)$在$t>1$时单调递增，从而当$t>1$时，$\varphi(t)>\varphi(1)=0$，命题成立．

综上所述，有$f'\left(\dfrac{x_1+x_2}2\right)>0$，因此原命题得证．

思考与总结　齐次化方法的总的思路是将问题转化为单变量的函数问题．

对称化方法　利用方程$k=x^2\ln x$研究函数的零点，由 $$(x^2\ln x)'_x=x(1+2\ln x),$$ 可得$k\in\left(-\dfrac{1}{2{\rm e}},0\right)$．函数$f(x)$的导函数 $$f'(x)=1+\ln x+\dfrac{k}{x^2}.$$ 由于$k<0$，因此$f'(x)$单调递增，设其唯一零点为$x_0$，则 $$1+\ln x_0+\dfrac{k}{x_0^2}=0,$$ 只需要证明$x_1+x_2\neq 2x_0$即可．构造函数$g(x)=f(x)-f(2x_0-x)$，$x\in (0,x_0]$，则其导函数 $$\begin{split} g'(x)&=f'(x)+f'(2x_0-x)\\ &=\ln\left[x(2x_0-x)\right]+k\left[\dfrac{1}{x^2}+\dfrac{1}{(2x_0-x)^2}\right]+2\\ &<\ln\left[\dfrac{x+(2x_0-x)}{2}\right]^2+k\cdot \dfrac{(1+1)^3}{\left[x+(2x_0-x)\right]^2}+2\\& =2\left(\ln x_0+\dfrac{k}{x_0^2}+1\right) \\ &=2f'(x_0)=0,\end{split}$$ 因此在$(0,x_0)$上有$g(x)$单调递减，从而$g(x)>g(x_0)=0$，不妨设$x_1<x_2$，于是 $$f(x_2)=f(x_1)>f(2x_0-x_1),$$ 而$f(x)$在$(x_0,+\infty)$上单调递增，于是$x_2>2x_0-x_1$，从而$x_1+x_2>2x_0$，命题得证．

思考与总结　注意代数式结构以及取等条件大胆进行放缩．

构造函数方法　将问题转化为证明$x_1+x_2\neq 2x_0$后，考虑到 $$f''(x)=\dfrac 1x-\dfrac{2k}{x^3},$$ 构造函数 $$h(x)=f(x)-\left[\dfrac 12f''(x_0)(x-x_0)^2+f(x_0)\right],$$ 则其二阶导函数 $$h''(x)=f''(x)-f''(x_0)=\dfrac 1x-\dfrac{2k}{x^3}-\dfrac{1}{x_0}+\dfrac{2k}{x_0^3}=\dfrac{(x-x_0)\left[2k(x^2+x_0x+x_0^2)-x_0^2x^2\right]}{x^3x_0^3}.$$ 考虑到$k<0$，于是$2k(x^2+x_0x+x_0^2)-x_0^2x^2<0$，因此在$(0,x_0)$上$h''(x)>0$，在$(x_0,+\infty)$上$h''(x)<0$，结合$h''(x_0)=0$可得在$(0,+\infty)$上$h'(x)\leqslant 0$，又$h(x_0)=0$，因此在$(0,x_0)$上$h(x)>0$，在$(x_0,+\infty)$上$h(x)<0$，如图．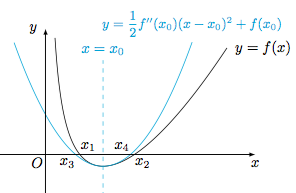
这样就有$f(x)$的两个零点$x_1,x_2$($x_1<x_2$)和二次函数$y=\dfrac 12f''(x_0)(x-x_0)^2+f(x_0)$的两个零点$x_3,x_4$($x_3<x_4$)满足 $$x_3<x_1<x_4<x_2,$$ 进而 $$x_1+x_2>x_3+x_4=2x_0,$$ 原命题得证．

思考与总结　通过构造二次函数的方法处理极值点偏移问题可以有效减少运算量．