本题改编自2009年复旦千分考试题:
若两条曲线$f,g$在公共点$P$处的切线互相垂直,那么称这两条曲线正交于点$P$.已知$AB$是单位圆$D$的一条弦,称与单位圆$D$同时正交于点$A$和点$B$的圆弧$AB$为$D$的曲弦,记作$(AB)$.当$AB$是单位圆$D$的直径时,定义曲弦$(AB)$为直径$AB$.下列说法错误的是( )
A.存在曲弦$(AB)$,使得对单位圆内部任意一点$P$,均存在过$P$的曲弦$(CD)$与$(AB)$正交于某点
B.若曲弦$(AB)$与曲弦$(CD)$相切,那么切点一定在单位圆上
C.存在曲弦$(AB)$和曲弦$(CD)$,它们恰好有两个公共点
D.对任意曲弦$(AB)$和不在曲弦$(AB)$上的单位圆内部一点$P$,均存在曲弦$(CD)$经过点$P$且与$(AB)$没有公共点
分析与解 逐步深入地进行思考.
思考一 曲弦是个什么东西?
过圆外一点$O'$引圆的两条切线$O'P$和$O'Q$,那么以$O'$为圆心,切线长为半径作圆被单位圆所截的圆弧$PQ$即为曲弦.
思考二 如何作过指定点的一条曲弦?
当指定点$A$位于单位圆上时,作图是简单的.只需要作过$A$的单位圆的切线,那么切线上任意一点$O'$为圆心,$O'A$为半径作圆被单位圆所截得的圆弧即为过点$A$的曲弦;
当指定点$A$在单位圆内时,问题就复杂一些了.
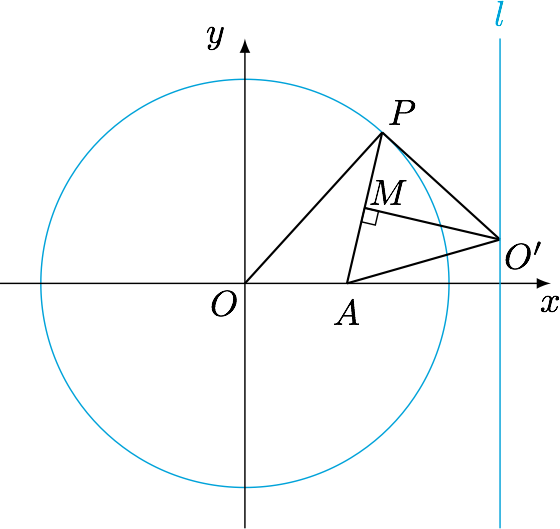
不妨设$A(a,0)$,$P$为单位圆上任意一点,那么$P$处单位圆的切线与线段$AP$的垂直平分线的交点$O'$即为过点$A,P$的曲弦的圆心.利用解析几何知识可得$O'$的轨迹是直线$x=\dfrac 12\left(a+\dfrac 1a\right)$.
这就意味着,只要作出单位圆内一点$A$对应的直线$l(A)$,在$l(A)$上任取一点$O'$作为圆心,$O'A$为半径作圆被单位圆所截得的圆弧即为过点$A$的曲弦.
思考三 如何作过指定两点的一条曲弦?
继续前面的思考.当指定两点$A,B$与圆心$O$不共线时,作直线$l(A)$和$l(B)$,取其交点为曲弦圆心即可;当指定两点$A,B$与圆心$O$共线(包含其中一点为$O$的情形)时,过$A,B$的直径即为所求曲弦.
接下来,我们来看看选项.
对于选项A,取直径$AB$,从点$A$出发作一系列与$AB$垂直的曲弦,最后汇聚到$B$,如图.
这些曲弦会经过圆内的任何一点,因此命题成立;
对于选项B,如果两条曲弦相切于圆内一点$A$,那么它们的圆心必然同在直线$l(A)$上,此时$A\notin l(A)$,因此与两条曲弦相切矛盾,因此命题成立;
对于选项C,根据思考三,命题错误;
对于选项D,与对选项A的思考类似,对任意曲弦$(AB)$,我们都可以作一系列曲弦$(CD)$(保持$CD\parallel AB$),而这一系列曲弦$(CD)$将扫过整个单位圆及其内部,因此命题成立.
因此正确答案是C.
注一 对于选项A,事实上有:对任意曲弦$(AB)$及单位圆内部任意一点$P$,均存在过$P$的曲弦$(CD)$与$(AB)$正交于某点.
注二 对于选项C,可以用解析的方法解决.设曲弦所在的圆的方程为$$(x-m)^2+(y-n)^2=m^2+n^2-1,$$则$$2mx+2ny=x^2+y^2+1,$$于是在给定两点$(x_1,y_1)$和$(x_2,y_2)$,且这两点连线不经过原点的情况下,圆心坐标就确定了(二元一次方程组的解);这两点连线经过原点时,曲弦为直径,也唯一确定,因此命题错误.