A-L-G不等式的内容是:\[\forall a,b>0\land a\neq b,\sqrt{ab}<\dfrac{a-b}{\ln a-\ln b}<\dfrac{a+b}2.\]
A-L-G不等式(对数—平均值不等式)描述了我们在解导数中的不等式问题中常见的\(\ln\dfrac{x_1}{x_2}\)的上下界,因此是处理该类问题的利器,如 每日一题[78] 对数函数的齐次化构造 ,每日一题[83] 有关\(x_1+x_2\)导函数不等式的对称化构造,对数函数不等式的化齐次方法,等等.
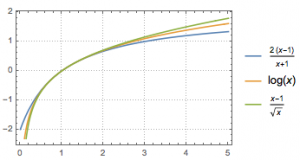
证明 不妨设\(a>b\),令\(x=\dfrac ab\),则欲证不等式等价于\[\forall x>1,\dfrac{2(x-1)}{x+1}<\ln x<\dfrac{x-1}{\sqrt x}.\]
注意到当\(x=1\)时三者均为\(0\),于是只需要证明\[\forall x>1, \left(\dfrac{2(x-1)}{x+1}\right)'<\left(\ln x\right)'<\left(\dfrac{x-1}{\sqrt x}\right)',\]以下略.
注 这个函数不等式比常用函数不等式\[\forall x>0,\ln x\leqslant x-1\]精细得多.
下面给出一个简单的例子.
(2015年吉林省长春市四模题)已知函数\(f(x)={\rm e}^x-ax\)有两个零点\(x_1<x_2\),则下列说法错误的是( )
A.\(a>{\rm e}\)
B.\(x_1+x_2>2\)
C.\(x_1x_2>1\)
D.有极小值点\(x_0\),且\(x_1+x_2<2x_0\)
解 函数\(f(x)\)的导函数为\[f'(x)={\rm e}^x-a,\]于是有极小值点\(x=\ln a\),而极小值为\(a\left(1-\ln a\right)\).于是根据题意,极小值应小于\(0\),从而\(a>{\rm e}\),选项 A 正确.下面分析选项 B、C、D.
根据题意有\[\begin{eqnarray}\begin{split}x_1=\ln a+\ln x_1,\\x_2=\ln a+\ln x_2,\end{split}\end{eqnarray}\]
两式相减,得\[\dfrac{x_1-x_2}{\ln x_1-\ln x_2}=1,\]于是\[\sqrt{x_1x_2}<1<\dfrac{x_1+x_2}2,\]即\[x_1x_2<1\land x_1+x_2>2,\]选项 B 正确,而选项 C 错误.
选项 D:根据题意\(x_0=\ln a\),而根据(1),有\[x_1+x_2=2\ln a+\ln\left(x_1x_2\right),\]结合对选项 C 的分析,可知选项 D 正确.
综上,符合题意的选项为 C.