已知函数\(f(x)=x\ln x\)与直线\(y=m\)交于\(A\left(x_1,y_1\right)\)、\(B\left(x_2,y_2\right)\)两点.
(1)求证:\(0<x_1x_2<\dfrac{1}{{\mathrm e}^2}\);
(2)求证:\(\dfrac{2}{\mathrm e}<x_1+x_2<1\).
 对于第一小问,可以猛击 每日一题[78] 对数函数的齐次化构造 .
对于第一小问,可以猛击 每日一题[78] 对数函数的齐次化构造 .
由\(x_1\ln{x_1}=m\),\(x_2\ln{x_2}=m\)可得\[\ln{x_1}=\dfrac{m}{x_1},\ln{x_2}=\dfrac{m}{x_2},\]两式分别相加和相减可得\[\begin{split}\ln\left(x_1x_2\right)&=\dfrac{m\left(x_1+x_2\right)}{x_1x_2},\qquad\cdots (1)\\\ln\dfrac{x_1}{x_2}&=\dfrac{m\left(x_2-x_1\right)}{x_1x_2},\qquad \cdots (2)\end{split}\]从(2)式中解出\(m\)带入(1),有\[\ln\left(x_1x_2\right)=\ln\dfrac{x_1}{x_2}\cdot\dfrac{x_1+x_2}{x_2-x_1}.\] 由常用放缩\[\forall x\in (0,1),\ln x<2\cdot\dfrac{x-1}{x+1},\]不妨设\(x_1<x_2\)可得\[\ln\dfrac{x_1}{x_2}<2\cdot\dfrac{x_1-x_2}{x_1+x_2},\]两边同乘以\(\dfrac{x_1+x_2}{x_2-x_1}\)即得\[\ln\left(x_1x_2\right)<-2,\]于是\[0<x_1x_2<\dfrac{1}{{\mathrm e}^2}.\] 对于第二小问,首先研究函数图象如下. 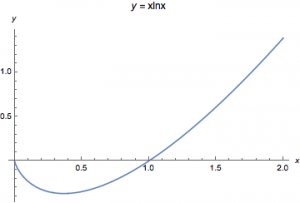 其中极小值点为\(x=\dfrac{1}{\mathrm e}\),于是\(0<x_1<\dfrac{1}{\mathrm e}<x_2<1\),且函数在\(\left(0,\dfrac{1}{\mathrm e}\right)\)上单调递减,在\(\left(\dfrac{1}{\mathrm e},1\right)\)上单调递增.
其中极小值点为\(x=\dfrac{1}{\mathrm e}\),于是\(0<x_1<\dfrac{1}{\mathrm e}<x_2<1\),且函数在\(\left(0,\dfrac{1}{\mathrm e}\right)\)上单调递减,在\(\left(\dfrac{1}{\mathrm e},1\right)\)上单调递增.
对于欲证不等式的左边,不妨设\(x_1=\dfrac{1}{\mathrm e}-x\),其中\(0<x<\dfrac{1}{\mathrm e}\),那么我们只需要证明\[x_2>\dfrac{1}{\mathrm e}+x,\]而\(\dfrac{1}{\mathrm e}<\dfrac{1}{\mathrm e}+x<1\),函数在\(\left(\dfrac{1}{\mathrm e},1\right)\)上单调递增,于是只需要证明\[f\left(x_2\right)>f\left(\dfrac{1}{\mathrm e}+x\right),\]事实上\[f\left(x_2\right)=f\left(x_1\right)=f\left(\dfrac{1}{\mathrm e}-x\right),\]于是问题转化为证明\[\forall x\in \left(0,\dfrac{1}{\mathrm e}\right),f\left(\dfrac{1}{\mathrm e}-x\right)>f\left(\dfrac{1}{\mathrm e}+x\right).\] 接下来就是常规的恒成立问题了,留给读者.
对于欲证不等式的右边,需要小小的处理一下.
情形1:当\(0<x_1<\dfrac{1}{\mathrm e}<x_2\leqslant \dfrac{1}{2}\)时,命题显然成立;
情形2:假设\(0<x_1<\dfrac{1}{\mathrm e}\),\(\dfrac{1}{2}<x_2<1\),则不妨设\(x_2=\dfrac{1}{2}+x\),其中\(0<x<\dfrac{1}{2}\).此时只需要证明\[x_1<\dfrac{1}{2}-x.\]
1° 当\(0<x\leqslant\dfrac{1}{2}-\dfrac{1}{\mathrm e}\)时,由于\(0<x_1<\dfrac{1}{\mathrm e}\),所以命题显然成立.
2° 当\(\dfrac{1}{2}-\dfrac{1}{\mathrm e}<x<\dfrac{1}{2}\)时,\(0<\dfrac{1}{2}-x<\dfrac{1}{\mathrm e}\),函数在\(\left(0,\dfrac{1}{\mathrm e}\right)\)上单调递减,因此只需要证明\[f\left(x_1\right)>f\left(\dfrac{1}{2}-x\right),\]事实上\[f\left(x_1\right)=f\left(x_2\right)=f\left(\dfrac{1}{2}+x\right),\]于是问题转化为证明\[\forall x\in \left(\dfrac{1}{2}-\dfrac{1}{\mathrm e},\dfrac{1}{2}\right),f\left(\dfrac{1}{2}+x\right)>f\left(\dfrac{1}{2}-x\right).\]
接下来还是常规的恒成立问题,继续留给读者.
2015年11月15日补充练习题. 已知$f(x)=x-a {\rm e} ^x$,其中$a\in\mathcal R$.
(1)讨论函数$f(x)$的单调性;
(2)若$f(x) \leqslant {\rm e} ^{2x}$任意实数$x$成立,求$a$的取值范围;
(3)若$f(x)$有两个不同零点$x_1$、$x_2$,求证:$x_1+x_2>2$.
答案 (1)当$a \leqslant 0$时,$f(x)$在$\mathcal R$上单调递增; 当$a>0$,$f(x)$在$\left(-\infty ,\ln \dfrac 1a\right)$上单调递增,在$\left (\ln \dfrac 1a,+\infty \right) $上单调递减.
(2)$a \geqslant -1$.
(3)略.

请问下能否证明x1•x2•(x1+x2) < 2/(e^3) 呢?最近在一本书上看到这个命题 但没有给证明qaq
Pingback引用通告: 每日一题[490]另类的比较大小(导数) | 数海拾贝内容系统
Pingback引用通告: 每日一题[490]另类的比较大小 | Math173
Pingback引用通告: 每周一招[8]对数-平均值不等式(A-L-G不等式)(高二) | 数海拾贝内容系统
Pingback引用通告: 每日一题[433]极值点偏移法 | Math173
Pingback引用通告: 每日一题[433]极值点偏移法 | 数海拾贝内容系统
Pingback引用通告: 每日一题[432]极值点偏移与对称化构造 | 数海拾贝内容系统
Pingback引用通告: 每日一题[432]极值点偏移与对称化构造 | Math173
最后的那个恒成立似乎不太好证吧?对于x→1/2的处理,似乎要用洛必达...高考不能用
不需要,请仔细思考.
直接证明-X1>f(X1)=f(X2)>X2-1可能简单一点吧
x1+x2<1好像忘记证了哦