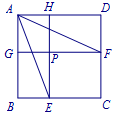
如图，在正方形\(ABCD\)中，被两条与边平行的线段\(EH、GF\)分割成四个小矩形，\(P\)是\(EH\)与\(GF\)的交点，若矩形\(PECF\)的面积恰是矩形\(AGPH\)的\(2\)倍，试确定\(\angle FAE\)的大小．
分析 在《角含半角模型之90°含45°（一）》，《角含半角模型之90°含45°（二）》，《角含半角模型之90°含45°（三）》之后，很明显的看出此题是角含半角模型，那么遇见此类问题马上会想到旋转全等，想法很丰满，现实很骨干，这两个三角形全等中缺少条件去判定．所以我们要根据已知中的面积\(2\)倍，去求得第三边等，此题才能解决．
解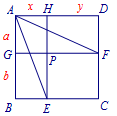 
设\(AG=a，GB=b，AH=x，HD=y\)， 根据题意可得\[a+b=x+y，2ax=by,\]则\((a-x)^2=(y-b)^2\)，将\(2ax=by\)代入可得\[(a+x)^2=y^2+b^2,\]
将\(CB\)延长，使得\(BQ=DF\)，连接\(AQ\)、\(EF\)， 所以\[EF=EQ,\] 所以\[\triangle AEF\cong \triangle AEQ,\] 可得\[\angle EAF=45^\circ.\]