在做解析几何习题时，容易陷入任何问题首先就设直线方程以及直线与圆锥曲线的交点坐标，然后联立直线方程与圆锥曲线方程的一个僵硬套路中去．可以看出，这种解题方式其实是“动直线驱动”的．事实上，有很多问题可以直接由“动点驱动”，也就是说对这类问题直接引入参数表达动点要比表达动直线更加直接．下面就通过一些“动点”驱动的例题诠释这一技巧．
例1、(2014年北京西城二模）已知椭圆\(W:\dfrac{x^2}2+y^2=1\)，直线\(l\)与\(W\)相交于\(M\)、\(N\)两点，\(l\)与\(x\)轴、\(y\)轴分别交于\(C\)、\(D\)两点，\(O\)为坐标原点．
（1）若直线\(l\)的方程为\(x+2y-1=0\)，求三角形\(OCD\)外接圆的方程；
（2）判断是否存在直线\(l\)，使得\(C\)、\(D\)是线段\(MN\)的两个三等分点，若存在，求出直线\(l\)的方程；若不存在，请说明理由．
解 （1）三角形\(OCD\)外接圆的方程为\[\left(x-\dfrac 12\right)^2+\left(y-\dfrac 14\right)^2=\dfrac 5{16}.\]
（2）设\(C(m,0)\)，\(D(0,n)\)则\(M(-m,2n)\)，\(N(2m,-n)\)．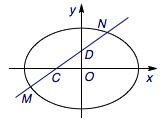
于是\[\begin{cases}\dfrac{m^2}2+4n^2=1,\\2m^2+n^2=1,\end{cases}\]解得\[m^2=\dfrac 25,\\n^2=\dfrac 15.\]
由截距式方程易得直线\(l\)的方程是\[l:y=\pm\dfrac{\sqrt 2}2x+\dfrac{\sqrt 5}5\lor y=\pm\dfrac{\sqrt 2}2x-\dfrac{\sqrt 5}5.\]
例2、（2014年北京海淀二模）已知椭圆\(G\)的离心率为\(\dfrac{\sqrt 2}2\)，其短轴两端点为\(A(0,1)\)，\(B(0,-1)\)．
（1）求椭圆\(G\)的方程；
（2）若\(C\)、\(D\)是椭圆\(G\)上关于\(y\)轴对称的两个不同点，直线\(AC\)、\(BD\)与\(x\)轴分别交于点\(M\)、\(N\)．判断以\(MN\)为直径的圆是否过点\(A\)，并说明理由．
解 （1）\(\dfrac{x^2}2+y^2=1\)；
（2）以\(MN\)为直径的圆不可能过点\(A\)，证明如下．
设\(C\left(\sqrt 2\cos\theta,\sin\theta\right)\)，\(D\left(-\sqrt 2\cos\theta,\sin\theta\right)\)，\(M(m,0)\)，\(N(n,0)\)，则由\(ACM\)和\(BND\)分别共线可得\[m=\dfrac{\sqrt 2\cos\theta}{1-\sin\theta},n=-\dfrac{\sqrt 2\cos\theta}{1+\sin\theta},\]于是\[mn=-\dfrac{\sqrt 2\cos^2\theta}{1-\sin^2\theta}=-\sqrt 2.\]
因此以\(MN\)为直径的圆恒过点\(\left(0,\pm\sqrt [4]2\right)\)，也就是说与\(y\)轴恒交于这两点，进而该圆不可能过\(y\)轴上的另外一点\(A\)．
另一方面，由于\(1<\sqrt [4]2\)，于是点\(A\)恒在以\(MN\)为直径的圆的内部．
例3、（2014年北京朝阳二模）已知椭圆\(C\)的中心在原点\(O\)，焦点在\(x\)轴上，离心率为\(\dfrac 12\)，右焦点到右顶点的距离为\(1\)．
（1）求椭圆\(C\)的标准方程；
（2）是否存在与椭圆\(C\)交于\(A\)、\(B\)两点的直线\(l:y=kx+m\)，使得\[\left|\overrightarrow{OA}+2\overrightarrow{OB}\right|=\left|\overrightarrow{OA}-2\overrightarrow{OB}\right|\]成立．若存在，求出实数\(m\)的取值范围；若不存在，请说明理由．
解 （1）椭圆\(C:\dfrac{x^2}4+\dfrac{y^2}3=1\)；
（2）设\(A\left(\cos\theta_1,\sqrt 3\sin\theta_1\right)\)，\(B\left(2\cos\theta_2,\sqrt 3\sin\theta_2\right)\)．
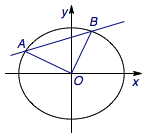由\[\left|\overrightarrow{OA}+2\overrightarrow{OB}\right|=\left|\overrightarrow{OA}-2\overrightarrow{OB}\right|\]得\[4\cos\theta_1\cos\theta_2+3\sin\theta_1\sin\theta_2=0.\qquad\cdots (*).\]而直线\(AB\)的截距\[m=\dfrac{\sqrt 3\sin\left(\theta_1-\theta_2\right)}{\cos\theta_2-\cos\theta_1}.\qquad\cdots (**).\]
令\(\theta_1+\theta_2=\alpha\)，\(\theta_1-\theta_2=\beta\)，则
由(*)得\[\cos\alpha+7\cos\beta=0,\]由(**)得\[m^2=3\cdot\dfrac{1+\cos\beta}{1-\cos\alpha},\]将上式代入，得\[m^2=\dfrac 37\cdot\left(1+\dfrac{6}{1-\cos\alpha}\right),\]因此\(m\)的取值范围是\(\left(-\infty,\sqrt{\dfrac{12}{7}}\right]\cup\left[\sqrt{\dfrac{12}{7}},+\infty\right)\)．
注 事实上，条件\[\left|\overrightarrow{OA}+2\overrightarrow{OB}\right|=\left|\overrightarrow{OA}-2\overrightarrow{OB}\right|\]即\(\overrightarrow{OA}\perp 2\overrightarrow{OB}\)，于是直线\(l\)为椭圆的姊妹圆之一\[x^2+y^2=\dfrac{1}{\dfrac 14+\dfrac 13}=\dfrac{12}7\]的切线，立得\(m\)的取值范围是\(\left(-\infty,\sqrt{\dfrac{12}{7}}\right]\cup\left[\sqrt{\dfrac{12}{7}},+\infty\right)\)．
最后给出一组练习．
练习1、（2014年北京海淀一模）已知\(A\)、\(B\)是椭圆\(C:2x^2+3y^2=9\)上两点，点\(M\)的坐标为\((1,0)\)．
（1）当\(A\)、\(B\)两点关于\(x\)轴对称，且三角形\(MAB\)为等边三角形时，求\(AB\)的长；
（2）当\(A\)、\(B\)两点不关于\(x\)轴对称时，证明：三角形\(MAB\)不可能为等边三角形．
练习2、（2014年北京通州二模）已知点\(Q\)为直线\(x=-4\)上的动点，过点\(Q\)作直线\(l\)垂直于\(y\)轴，动点\(P\)在直线\(l\)上，且满足\(OP\perp OQ\)（\(O\)为坐标原点），记动点\(P\)的轨迹为\(C\)．
（1）求曲线\(C\)的方程；
（2）设\(A\)、\(B\)为曲线\(C\)上的两点，且直线\(AB\)与\(x\)轴不垂直．若线段\(AB\)中点的横坐标为\(2\)，求证：线段\(AB\)的垂直平分线过定点．
练习3、已知\(A\)，\(B\)为椭圆\(\dfrac {x^2}8+\dfrac {y^2}2=1\)上的两点，弦\(AB\)的长为\(\dfrac 83\)，求三角形\(AOB\)的面积范围．
参考答案
练习1、（1）\(AB\)的长为\(\dfrac{14\sqrt 3}{9}\)或\(\dfrac{2\sqrt 3}3\)．（2）略．
提示 （2）证明椭圆上一点\(P\)到\(M\)的距离是关于\(P\)点横坐标的单调函数即可．
练习2、（1）曲线\(C:y^2=4x\)；（2）线段\(AB\)的垂直平分线过定点\((4,0)\)．
提示 （2）设\(A\left(4a^2,4a\right)\)，\(B\left(4b^2,4b\right)\)．
练习3、\(\left[\dfrac {8\sqrt 2}9,2\right]\)，http://lanqi.org/?p=438