圆锥曲线试题一则

这是2014年12月11日，我的学生朱怡洁问我的一道圆锥曲线试题：

已知$A$，$B$为椭圆$\dfrac {x^2}8+\dfrac {y^2}2=1$上的两点，弦$AB$的长为$\dfrac 83$，求三角形$AOB$的面积范围．

如果用常规的方法解运算繁杂，有没有运算较为简便的方法呢？

在这里我给出两种方法：

参数方程的方法

设$A(2\sqrt 2 \cos \theta_1,\sqrt 2 \sin \theta_1),B(2\sqrt 2\cos \theta_2,\sqrt 2 \sin \theta_2)$则

$$AB^2=8(\cos \theta_1-\cos \theta_2)^2+2(\sin \theta_1-\sin \theta_2)^2=\dfrac {64}9.$$

同时

$$S_{\triangle AOB}=\dfrac 12\left|2\sqrt 2 \cos \theta_1\cdot\sqrt 2 \sin \theta_2 -\sqrt 2 \sin \theta_1 \cdot2\sqrt 2\cos \theta_2\right|=2\left|\sin(\theta_1-\theta_2)\right|.$$

为了建立两个式子之间的联系，我们设

$$\alpha=\dfrac {\theta_1+\theta_2}2,\beta=\dfrac {\theta_1-\theta_2}2,$$ 那么经过和差化积，条件转化为

$$(3\sin^2\alpha+1)\sin^2\beta=\dfrac 89,$$

欲求面积转化为$2\left|\sin 2\beta\right|$．

接下来容易求得$\sin^2\beta$的范围，从而求得$2|\sin 2\beta|$的范围为$\left[\dfrac {8\sqrt 2}9,2\right]$．

---

仿射变换的方法

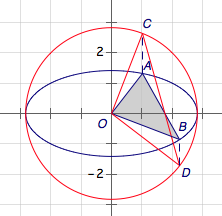
如图作变换，则椭圆变为圆心在原点，半径为$2\sqrt 2$的圆，设$A\to C,B\to D$，则

$$S_{\triangle AOB}=\dfrac 12S_{\triangle COD}.$$

而相比较而言，三角形$COD$的面积比较好求．

设$AB$的斜率为$k$，则由于$2b=2\sqrt 2>\dfrac 83$，因此$k\in \mathcal R$．

根据弦长公式，

$$\dfrac {CD}{AB}=\dfrac {\sqrt {1+4k^2}\cdot \left|x_C-x_D\right|}{\sqrt {1+k^2}\cdot \left|x_A-x_B\right|}=\sqrt {\dfrac {1+4k^2}{1+k^2}}.$$

因此$\dfrac 12CD$的取值范围为$\left[\dfrac 43,\dfrac 83\right]$.进而三角形$OCD$的面积为

$$\dfrac 12CD\cdot \sqrt {8-\left(\dfrac 12CD\right)^2}.$$ 不难算得其取值范围为$\left[\dfrac {16\sqrt 2}9,4\right]$．因此所求取值范围为$\left[\dfrac {8\sqrt 2}9,2\right]$．

一种是强硬的代数变形，另外一种是巧妙的几何转化，你更喜欢哪种呢？

---

2016年5月30日补充练习题．

已知椭圆$\dfrac{x^2}4+y^2=1$上两点$A,B$，且$\angle AOB=60^\circ$，求$\triangle AOB$面积的取值范围．

解    设$OA,OB$的斜率分别为$k_1,k_2$，则

$$\dfrac{|k_1-k_2|}{1+k_1k_2}=\sqrt 3.$$ 作仿射变换 $$x'=x,y'=2y,$$ 点$A,B$变为$A',B'$，则$OA',OB'$的斜率分别为$2k_1,2k_2$，设$\angle A'OB'=\theta$，则 $$S_{\triangle AOB}=\dfrac 12S_{\triangle A'OB'}=\sin\theta.$$ 考虑 $$|\tan \theta|=\dfrac{|2k_1-2k_2|}{1+4k_1k_2}=\dfrac{\sqrt 3}2\cdot \left|\dfrac{1+k_1k_2}{\dfrac 14+k_1k_2}\right|.$$

由

$$\dfrac{|k_1-k_2|}{1+k_1k_2}=\sqrt 3$$ 不难求出$k_1k_2$的取值范围是$k_1k_2\leqslant -3$或$k_1k_2\geqslant -\dfrac 13$．这样，可得$|\tan\theta|$的取值范围是$\left[\dfrac{4\sqrt  3}11,+\infty\right)$，于是$\sin\theta$的取值范围是$\left[\dfrac{4\sqrt 3}{13},1\right]$，也即$\triangle AOB$面积的取值范围是$\left[\dfrac{4\sqrt 3}{13},1\right]$．