三次函数$f\left( x \right) = a{x^3} + b{x^2} + cx + d$($a \ne 0$)在高中阶段学习导数后频繁出现,同时也是其他复杂函数的重要组成部分,因此有必要对其性质有所了解,才可以做到知己知彼,百战不殆.
性质一 单调性
以$a>0$为例,如图1,记$\Delta=b^2-3ac$为三次函数图象的判别式,则
当$\Delta \leqslant 0$时,$f(x)$为$\mathcal R$上的单调递增函数; 当$\Delta >0$时,$f(x)$会在中间一段单调递减,形成三个单调区间以及两个极值.
性质一的证明 $f(x)$的导函数为$$f'(x)=3ax^2+2bx+c,$$其判别式为$4(b^2-3ac)$,进而易得结论.
性质二 对称性
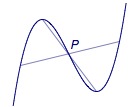
如图2,$f\left( x \right)$的图象关于点$P\left( { - \dfrac{b}{{3a}} , f\left( { - \dfrac{b}{{3a}}} \right)} \right)$对称(特别地,极值点以及极值点对应的图象上的点也关于$P$对称).
反之,若三次函数的对称中心为$\left( {m , n} \right)$,则其解析式可以设为$$f\left( x \right) = \alpha\cdot{\left( {x-m} \right)^3} + \beta \cdot \left( {x-m} \right) + n,$$其中$\alpha\neq 0$.
性质二的证明 由于$$f(x)=a\left(x+\dfrac b{3a}\right) ^3+\left( c-\dfrac{b^2}{3a}\right) \left( x+\dfrac b{3a}\right) -\dfrac{bc}{3a}+\dfrac{2b^3}{27a^2}+d,$$即$$f(x)=a\left(x+\dfrac b{3a}\right) ^3+\left( c-\dfrac{b^2}{3a}\right) \left( x+\dfrac b{3a}\right)+f\left( -\dfrac{b}{3a}\right) ,$$于是性质二得证.
例1 设直线$l$与曲线$y = {x^3} + x + 1$有三个不同的交点$A , B , C$,且$\left| {AB} \right| = \left| {BC} \right| = \sqrt 5 $,求直线$l$的方程.
解 由$|AB|=|BC|$可知$B$为三次函数的对称中心,由性质二可得$B(0,1)$,进而不难求得直线$l$的方程$y=2x+1$.
例2 设函数$f\left( x \right) = x\left( {x-1} \right)\left( {x-a} \right)$,$a > 1$.
(1)求导数$f'\left( x \right)$,并证明$f\left( x \right)$有两个不同的极值点${x_1} $,${x_2}$;
(2)若不等式$f\left( {{x_1}} \right) + f\left( {{x_2}} \right) \leqslant 0$成立,求$a$的取值范围.
(1)解 $f(x)$的导函数$$\begin{split} f'(x)&=(x-1)(x-a)+x(x-a)+x(x-1)\\&=3x^2-2(a+1)x+a, \end{split} $$而$$\begin{split} f'(0)&=a>0,\\f'(1)&=1-a<0,\\f'(a)&=a(a-1)>0, \end{split} $$于是$f'(x)$有两个变号零点,从而$f(x)$有两个不同的极值点.
(2)解 根据性质二,三次函数的对称中心$\left(\dfrac{a+1}3,f \left( \dfrac{a+1}3\right)\right) $是两个极值点对应的函数图象上的点的中点.于是$$f(x_1)+f(x_2)=2f\left(\dfrac{a+1}3\right)\leqslant 0,$$即$$2\cdot\dfrac{a+1}3\cdot\dfrac{a-2} 3\cdot\dfrac{-2a+1}3\leqslant 0,$$结合$a>1$,可得$a$的取值范围是$[2,+\infty )$.
注 本题为2004年高考重庆卷理科数学第$20$题.
性质三 切割线性质
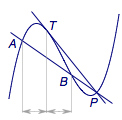
如图3,设$P$是$f\left( x \right)$上任意一点(非对称中心),过$P$作函数$f\left( x \right)$图象的一条割线$AB$与一条切线$PT$($P$点不为切点),$A$、$B$、$T$均在$f\left( x \right)$的图象上,则$T$点的横坐标平分$A$、$B$点的横坐标.
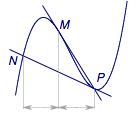
推论1 设$P$是$f\left( x \right)$上任意一点(非对称中心),过$P$作函数$f\left( x \right)$图象的两条切线$PM$、$PN$,切点分别为$M$、$P$,如图.则$M$点的横坐标平分$P$、$N$点的横坐标,如图4.
推论2 设$f\left( x \right)$的极大值为$M$,方程$f\left( x \right) = M$的两根为${x_1}$、${x_2}$(${x_1} < {x_2}$),则区间$\left[ {{x_1} , {x_2}} \right]$被$ - \dfrac{b}{{3a}}$和极小值点三等分.
性质三的证明 设$f(x)=ax^3+bx^2+cx+d$($a\ne 0$),直线$PT:y=k_0x+m_0$,直线$PAB:y=kx+m$,则分别将直线$PT$与直线$PAB$的方程与三次函数的解析式联立,得$$\begin{split} ax^3+bx^2+(c-k_0)x+d-m_0=0,\\ax^3+bx^2+(c-k)x+d-m=0, \end{split} $$于是根据三次方程的韦达定理可得$$2x_T+x_P=x_A+x_B+x_P,$$即$$x_T=\dfrac{x_A+x_B}2,$$于是命题得证. 推论1和推论2的证明留给读者.
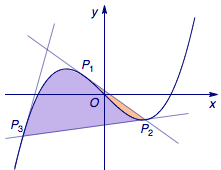
例3 如图6,记三次函数$f(x)=ax^3+bx^2+cx+d$($a\neq 0$)的图象为$C$,若对于任意非零实数$x_1$,曲线$C$与其在点$P_1\left(x_1,f(x_1)\right) $处的切线交于另一点$P_2\left(x_2,f(x_2)\right)$,曲线$C$与其在点$P_2$处的切线交于另一点$P_3\left(x_3,f(x_3)\right)$,线段$P_1P_2$、$P_2P_3$与曲线$C$所围成的封闭图形的面积分别记为$S_1$、$S_2$.求证:$\dfrac{S_1}{S_2}$是定值.
解 由性质二,任意三次函数$f(x)$都可以通过平移变化变成$$g(x)=px^3+qx,$$然后可以作伸缩变换变成$$h(x)=x^3+rx,$$而无论平移还是伸缩,题中的$\dfrac{S_1}{S_2}$均保持不变,因此只需要证明命题对三次函数$h(x)=x^3+rx$成立即可. 根据题意,联立函数$h(x)=x^3+rx$与函数$h(x)$在$P_1$处的切线方程得$$(x-x_1)^2\cdot (x-x_2)=0,$$于是$$2x_1+x_2=0,$$即$$x_2=-2x_1.$$又由性质三的推论1,可得$$2x_1=x_2+x_3,$$即$$x_3=4x_1.$$ 于是,线段$P_1P_2$与曲线$C$所围成的封闭图形的面积$$\begin{split} S_1&=\left|\int_{x_1}^{x_2}{(x-x_1)^2\cdot (x-x_2)}{\rm d}x\right|\\&=\left|\int_{x_1}^{-2x_1}{\left(x^3-3x_1^2x+2x_1^3\right)}{\rm d}x\right|\\&=\left|\left.\left(\dfrac 14x^4-\dfrac 32x_1^2x^2+2x_1^3x\right)\right|_{x_1}^{-2x_1}\right|\\&=\dfrac{27}4x_1^4,\end{split} $$类似的,线段$P_2P_3$与曲线$C$所围成图形的面积$$S_2=\dfrac{27}4x_2^4,$$于是所求的面积之比为$$\dfrac{S_1}{S_2}=\left(\dfrac{x_1}{x_2}\right)^4=\dfrac 1{16}.$$
注 此题即2010年高考福建卷理科数学第20题第(2)小问(第(1)小问要求证明该结论对$f(x)=x^3-x$成立).
性质四 切线条数
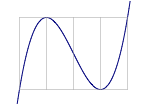
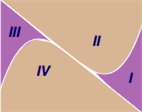
如图7,过$f\left( x \right)$的对称中心作切线$l$,则坐标平面被切线$l$和函数$f\left( x \right)$的图象分割为四个区域,有以下结论:
① 过区域 I、III 内的点作$y = f\left( x \right)$的切线,有且仅有三条; ② 过区域 II、IV 内的点以及对称中心作$y = f\left( x \right)$的切线,有且仅有一条; ③ 过切线$l$或函数$f\left( x \right)$图象(除去对称中心)上的点作$y = f\left( x \right)$的切线,有且仅有两条.
性质四的证明 由性质二,不妨设$f(x)=x^3+mx$,坐标平面内一点$P(a,b)$. 三次函数图象上$x=t$处的切线方程为$$y=(3t^2+m)(x-t)+t^3+mt,$$即$$y=(3t^2+m)x-2t^3,$$切线过点$P(a,b)$,即$$b=-2t^3+3at^2+ma.$$ 而三次函数对称中心处的切线方程为$$y=mx,$$于是考虑直线$y=b-ma$与函数$$h(t)=-2t^3+3at^2$$的图象公共点个数. 函数\(h(t)\)的零点为\(0\)和\(\dfrac {3a}{2}\),且\(0\)为它的一个极值点,由性质二的推论2知,\(h(t)\)的另外一个极值点对应的函数图象上的点的坐标为\((a,a^3)\),以\(a>0\)为例,\(h(t)\)的草图如下: 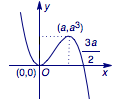 容易得到结论: 当$a<0$时,$b<a^3+ma\lor b>ma$时为$1$个公共点,$b=ma\lor b=a^3+ma$时为$2$个公共点,$a^3+ma<b<ma$时为$3$个公共点; 当$a=0$时,无论$b$取何值,均为$1$个公共点; 当$a>0$时,$b>a^3+ma\lor b<ma$时为$1$个公共点,$b=ma\lor b=a^3+ma$时为$2$个公共点,$ma<b<a^3+ma$时为$3$个公共点. 综上,性质四得证.
容易得到结论: 当$a<0$时,$b<a^3+ma\lor b>ma$时为$1$个公共点,$b=ma\lor b=a^3+ma$时为$2$个公共点,$a^3+ma<b<ma$时为$3$个公共点; 当$a=0$时,无论$b$取何值,均为$1$个公共点; 当$a>0$时,$b>a^3+ma\lor b<ma$时为$1$个公共点,$b=ma\lor b=a^3+ma$时为$2$个公共点,$ma<b<a^3+ma$时为$3$个公共点. 综上,性质四得证.
在高考中,对结论 ① 的考察最为常见,例如2007年高考全国II卷理科数学第22题(压轴题)就是证明性质四的结论 ①:
已知函数$f\left( x \right) = {x^3} - x$.
(1)求曲线$y = f\left( x \right)$在点$M\left( {t , f\left( t \right)} \right)$处的切线方程;
(2)设$a > 0$,如果过点$\left( {a , b} \right)$可作曲线$y = f\left( x \right)$的三条切线,证明:$ - a < b < f\left( a \right)$.
例4 设函数$f\left( x \right) = \dfrac{1}{3}{x^3} - \dfrac{a}{2}{x^2} + bx + c$,其中$a > 0$.曲线$y = f\left( x \right)$在点$P\left( {0 , f\left( 0 \right)} \right)$处的切线方程为$y = 1$.
(1)确定$b,c$的值;
(2)设曲线$y = f\left( x \right)$在点$\left( {{x_1} , f\left( {{x_1}} \right)} \right)$及$\left( {{x_2} , f\left( {{x_2}} \right)} \right)$处的切线都过点$\left( {0 , 2} \right)$.证明:当${x_1} \neq {x_2}$时,$f'\left( {{x_1}} \right) \ne f'\left( {{x_2}} \right)$;
(3)若过点$\left( {0 , 2} \right)$可作曲线$y = f\left( x \right)$的三条不同切线,求$a$的取值范围.
解 (1)$f(x)$的导函数为$$f'(x)=x^2-ax+b,$$于是该函数在$x=0$处的切线方程为$$y=bx+c,$$因此$$b=0,c=1.$$ (2)函数$f(x)$在$x=t$处的切线方程为$$y=(t^2-at)(x-t)+\dfrac 13t^3-\dfrac a2t^2+1,$$当切线过点$(0,2)$时可得$$\dfrac 23t^3-\dfrac a2t^2+1=0,$$于是$x_1,x_2$是该方程的两个不等实根. 考虑$$\begin{split} f'(x_1)-f'(x_2)&=\left(x_1^2-ax_1\right)-\left(x_2^2-ax_2\right)\\&=\left(x_1-x_2\right)\cdot\left(x_1+x_2-a\right), \end{split} $$而$$\begin{cases} \dfrac 23x_1^3-\dfrac a2x_1^2+1=0,\\\dfrac 23x_2^3-\dfrac a2x_2^2+1=0,\end{cases} $$两式相减并约去$x_1-x_2$,得$$x_1^2+x_1x_2+x_2^2=\dfrac 34a^2,$$而$$\begin{split} x_1^2+x_1x_2+x_2^2&=(x_1+x_2)^2-x_1x_2\\&>(x_1+x_2)^2-\dfrac 14(x_1+x_2)^2\\&=\dfrac 34(x_1+x_2)^2, \end{split} $$于是$$x_1+x_2\neq a,$$进而可得$$f'(x_1)\ne f'(x_2).$$ (3)函数$f(x)$的对称中心为$\left(\dfrac a2,-\dfrac {a^3}{12}+1\right)$,于是在对称中心处的切线方程为$$y=-\dfrac{a^2}4\left(x-\dfrac a2\right)-\dfrac{a^3}{12}+1,$$根据性质四的结论 ①,可得$$1<2<\dfrac{a^3}{24}+1,$$解得$$a>2\sqrt[3]{3},$$即$a$的取值范围是$\left(2\sqrt[3]{3},+\infty \right)$.
注 此题为2010年高考湖北卷文科数学第21题(压轴题).
练习题
练习1、已知函数$f\left( x \right) = \dfrac{1}{3}{x^3} + a{x^2} + bx$,且$f'\left( { - 1} \right) = 0$.
(1)试用含$a$的代数式表示$b$;
(2)求$f\left( x \right)$的单调区间;
(3)令$a =-1$,设函数$f\left( x \right)$在$x_1,x_2$($x_1<x_2$)处取得极值,记点$M\left( {{x_1},f\left( {{x_1}} \right)} \right)$,$N\left( {{x_2},f\left( {{x_2}} \right)} \right)$,证明:线段$MN$与曲线$f\left( x \right)$存在异于$M$、$N$的公共点.
练习2、已知$f\left( x \right) = {x^3} + b{x^2} + cx + d$在$\left(- \infty , 0\right)$上是增函数,在$\left( {0 , 2} \right)$上是减函数,且方程$f\left( x \right) = 0$有三个根,它们分别为从小到大依次为$\alpha$、$2$、$\beta$.求$\left| {\alpha-\beta } \right|$的取值范围.
练习3、如图8,记原点为点${P_1}\left( {{x_1} , {y_1}} \right)$,由点${P_1}$向三次函数$y = {x^3} -3a{x^2} + bx$($a\neq 0$)的图象(记为曲线$C$)引切线,切于不同于点${P_1}$的点${P_2}\left( {{x_2} , {y_2}} \right)$,再由点${P_2}$引此曲线$C$的切线,切于不同于点${P_2}$的点${P_3}\left( {{x_3} , {y_3}} \right)$.如此继续作下去,得到点列$\left\{ {{P_n}\left( {{x_n} , {y_n}} \right)} \right\}$.试回答下列问题:
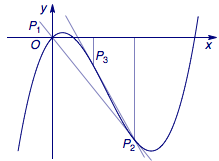
图8
(1)求数列$\{x_n\}$的递推公式与初始值;
(2)求$\lim\limits_{n \to+ \infty } {x_n}$,并指出点列$\{P_n\}$的极限位置在何处?
练习4、已知$f\left( x \right) = {x^3} - x$,过点$\left( {{x_0} , {y_0}} \right)$作$f\left( x \right)$图象的切线,如果可以作出三条切线,当${x_0} \in \left( {0 , 1} \right)$时,求点$\left( {{x_0} , {y_0}} \right)$所在的区域面积.
练习5、已知函数$f(x)=2x^3-3x$.
(1)求$f(x)$在区间$[-2,1]$上的最大值;
(2)若过点$P(1,t)$存在$3$条直线与曲线$y=f(x)$相切,求$t$的取值范围;
(3)问过点$A(-1,2)$,$B(2,10)$,$C(0,2)$分别存在几条直线与曲线$y=f(x)$相切?(只需写出结论)
练习6、已知函数$f(x)=\dfrac 13x^3+ax^2+bx$,且$f'(-1)=0$.
(1)试用含$a$的代数式表示$b$,并求$f(x)$的单调区间;
(2)令$a=-1$.设函数$f(x)$在$x_1,x_2$($x_1<x_2$)处取值极值,记点$M(x_1,f(x_1))$,$N(x_2,f(x_2))$,$P(m,f(m))$,$x_1<m \leqslant x_2$.请仔细观察曲线$f(x)$在点$P$处的切线与线段$MP$的位置变化趋势,并解答以下问题:
① 若对任意的$m\in (t,x_2]$,线段$MP$与曲线$f(x)$有异于$P$、$Q$的公共点,试确定$t$的最小值;
② 若存在点$Q(n,f(n))$,$x_1\leqslant n<m$,使得线段$PQ$与曲线$f(x)$有异于$P$、$Q$的公共点,请直接写出$m$的取值范围(不必写出求解过程).
练习题的参考答案
练习1、(1)$f(x)$的导函数为$$f'(x)=x^2+2ax+b,$$于是所求的代数表达式为$$b=2a-1.$$(2)在(1)的基础上,有$$f'(x)=(x+1)\cdot (x+2a-1),$$于是 当$a<1$时,函数$f(x)$的单调递增区间是$(-\infty ,-1)$和$(1-2a,+ \infty )$,单调递减区间为$(-1,1-2a)$; 当$a=1$时,函数$f(x)$的单调递增区间是$\mathcal R$; 当$a>1$时,函数$f(x)$的单调递增区间是$(-\infty,1-2a)$和$(-1,+\infty )$,单调递减区间是$(1-2a,-1)$.
(3)此时$$f(x)=\dfrac 13x^3-x^2-3x,$$而$$f'(x)=x^2-2x-3,$$于是$M\left(-1,\dfrac 53\right)$,$N\left( 3,-9\right) $.根据性质二,该公共点为三次函数$f(x)$图象的对称中心$\left(1,-\dfrac{11}3\right)$.
注 本题为2009年高考福建卷文科数学第21题(压轴题).
练习2、根据题意,$x=0$为$f(x)$的导函数$$f'(x)=3x^2+2bx+c$$的零点,于是$c=0$. 又$f(2)=0$,于是$$8+4b+d=0,$$即$$d=-4b-8,$$从而$$\begin{split} f(x)&=x^3+bx^2-(8+4b)\\&=(x-2)\cdot\left[x^2+(b+2)x+2b+4\right], \end{split} $$因此$$\left(\alpha-\beta\right)^2=\left(\alpha+\beta\right)^2-4\alpha\cdot\beta=(2-b)^2-16.$$ 另一方面,由$f(x)$在$(0,2)$上是减函数得$f'(2)\leqslant 0$,即$$12+4b \leqslant 0,$$于是可得$b$的取值范围是$$b<-3.$$ 从而$\left|\alpha-\beta\right|$的取值范围是$[3,+\infty)$.
练习3、(1) 根据已知,联立$P_1$出发的切线方程与曲线$C$的方程,得$$(x-x_1)(x-x_2)^2=0,$$又$x_1=0$,切线方程只能改变左边三次式的一次项和常数项,于是可得$$x_2=\dfrac 32a.$$ 进而由性质三的推论1可得$$\forall n\geqslant 3\land n\in\mathcal N^*,2x_n=x_{n-1}+x_{n-2}.$$ 于是数列$\{x_n\}$的递推公式与初始值为$$x_n=\dfrac{x_{n-1}+x_{n-2}}2,n\geqslant 3\land n\in\mathcal N^*,x_1=0,x_2=\dfrac 32a.$$(2)由数列的递推公式不难得到通项$$\forall n\in\mathcal N^*,x_n=a\cdot\left[1-\left(-\dfrac 12\right)^{n-1}\right],$$于是$$\lim_{n\to +\infty}x_n=a.$$因此点列$\{P_n\}$的极限位置为$(a,-2a^3+ab)$,也就是三次函数的对称中心.
练习4、函数$f(x)$在对称中心$(0,0)$处的切线方程为$$y=-x,$$于是根据性质四的结论 ①,我们可得所求区域面积为$$\int_{0}^{1}\left[x^3-x-(-x)\right]{\rm d}x=\int_0^1{x^3}{\rm d}x=\dfrac 14.$$
练习5、(1)$f(x)$的导函数$$f'(x)=6x^2-3,$$于是可得$f(x)$在区间$[-2,1]$上的最大值为$$\max\left\{f\left(-\dfrac{\sqrt 2}2\right),f(1)\right\}=\sqrt 2.$$ 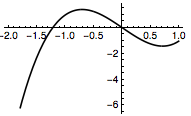 (2)函数$f(x)$在对称中心$(0,0)$处的切线方程为$$y=-3x,$$根据性质四的结论 ①,可得$$-3<t<f(1),$$即$$-3<t<-1,$$于是$t$的取值范围是$(-3,-1)$. (3)根据性质四,可得过$A(-1,2)$存在$3$条直线与曲线$y=f(x)$相切;过$B(2,10)$存在$2$条直线与曲线$y=f(x)$相切;过$C(0,2)$存在$1$条直线与曲线$y=f(x)$相切.
(2)函数$f(x)$在对称中心$(0,0)$处的切线方程为$$y=-3x,$$根据性质四的结论 ①,可得$$-3<t<f(1),$$即$$-3<t<-1,$$于是$t$的取值范围是$(-3,-1)$. (3)根据性质四,可得过$A(-1,2)$存在$3$条直线与曲线$y=f(x)$相切;过$B(2,10)$存在$2$条直线与曲线$y=f(x)$相切;过$C(0,2)$存在$1$条直线与曲线$y=f(x)$相切.
注 本题为2014年高考北京卷文科数学第20题(压轴题).
练习6、(1)$b=2a-1$; 当$a>1$时,函数$f(x)$的单调递增区间为$(-\infty ,1-2a)$和$(-1,+\infty )$,单调递减区间为$(1-2a,-1)$; 当$a=1$时,函数$f(x)$的单调递增区间为$\mathcal R$; 当$a<1$时,函数$f(x)$的单调递增区间为$(-\infty ,-1)$和$(1-2a,+ \infty )$,单调递减区间为$(-1,1-2a)$.  (2)① $t$的最小值为$2$,证明从略;② $m$的取值范围为$(1,3]$.
(2)① $t$的最小值为$2$,证明从略;② $m$的取值范围为$(1,3]$.
注 本题为2009年高考福建卷理科数学第21题(压轴题).

Pingback引用通告: 每日一题[832]三次函数的性质 | 数海拾贝内容系统
Pingback引用通告: 每日一题[832]三次函数的性质 | Math173
Pingback引用通告: 每日一题[705]三次函数的性质 | Math173
Pingback引用通告: [方法技巧]利用导函数研究函数的对称性 | 数海拾贝内容系统
性质四的证明中有几处错误:
1)“三次函数图象上x=t处的切线方程为
y=(3t2+m)(x−t)+t3+mt,
即
y=(3t2+m)x−3t3,”
应该为y=(3t2+m)x−2t3
2)判断交点的个数的范围和结论不对
例如在a>0时应当是:
当0<b-ma<a3时有三个交点,对应Ⅰ区域
当b-maa3时有一个交点,对应Ⅱ、Ⅳ区域
当b=ma或b=a3+ma时有两个交点,对应f(x)图像上和对称中心处切线上
嗯,抱歉,发布的版本不是最新的...