这是我在数海拾贝读者群里面看到的一道题:
设已知函数\(f(x)=\left|x-a\right|-\dfrac 4x+a,a\in\mathcal{R}\).是否存在实数\(a\),使得\(f(x)=3\)有且仅有\(3\)个不等实根,且它们成等差数列.若存在,求出所有\(a\)的值,若不存在,说明理由.
本题答案是\(a=-\dfrac{11}{6}\)或\(a=\dfrac{3}{2}\sqrt{3}+1\).
分析 因为\(f(x)\)的解析式含有绝对值,首先根据\(x\)的范围去绝对值得到\(f(x)\)的分段形式的表达式\[f(x)=\begin{cases}2a-\left(x+\dfrac 4x\right),x<a;\\x-\dfrac 4x,x\geqslant a.\end{cases}\]要研究\(f(x)=3\)的根的情况,就需要知道函数\(y=f(x)\)的图象与\(y=3\)的图象的交点情况.
我们先不考虑定义域的分段点,分别研究两段对应的函数在整个定义域上的情况:
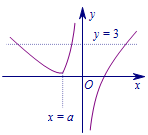
先研究不含参的函数,令\[h(x)=x-\dfrac 4x,\]则\(h(x)\)在\((-\infty,0)\)与\((0,+\infty)\)上分别单调递增,如图:
容易知道\(h(x)=3\)有两个根\(-1\)和\(4\);
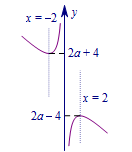
再研究另一个含参的函数,令\[g(x)=2a-\left(x+\dfrac 4x\right),\]由对勾函数的性质知\(g(x)\)有四个单调区间,分别为\((-\infty,-2),(-2,0),(0,2),(2,+\infty)\),草图如下:
其中\(x\)轴的位置由\(a\)的大小决定,结合图象知\(g(x)=3\)的根的个数可能为\(0,1,2\).
由题意知,\(y=f(x)\)的图象的“左半部分”(\((-\infty,a)\)的部分)由\(y=g(x)\)决定,“右半部分”(\([a,+\infty)\)的部分)由\(y=h(x)\)决定.\(f(x)=3\)有\(3\)个不相等的实数根,由前面对\(h(x)\)与\(g(x)\)的图象的分析知,左半部分与右半部分贡献的根的个数只可能有\(1,2\)和\(2,1\)两种情况.
情形一 若左半部分贡献\(1\)个根,则右半部分贡献两个根\(-1,4\),由三个根呈等差数列的条件知左半部分贡献的根为\(-6\),且有\(-6<a\leqslant -1\).于是有\[g(-6)=3,\]解得\[a=-\dfrac{11}{6}.\]此时\(f(x)\)的图象如下,容易验证此时满足题意:
情形二 若左半部分贡献\(2\)个根,则右半部分只贡献一个根\(4\),从而有\[-1\leqslant a<4.\]记左半部分贡献的根为\(x_1,x_2\),且\(x_1<x_2\),则有\[x_1+4=2x_2.\]且\(x_1,x_2\)是\(g(x)=3\)的两个根,化简得\(x_1,x_2\)为\[x^2+(3-2a)x+4=0\]的两根,于是有\[\begin{cases}x_1+x_2=2a-3,\\x_1x_2=4.\end{cases}\]联立\(x_1+4=2x_2\),解得\[\begin{cases}x_1=2(\sqrt 3-1),\\x_2=\sqrt 3+1,\\a=\dfrac 32\sqrt 3+1.\end{cases}\]或\[\begin{cases}x_1=-2(\sqrt 3+1),\\x_2=1-\sqrt 3,\\a=-\dfrac 32\sqrt 3+1.\end{cases}\]
因为\(-\dfrac 32\sqrt 3+1>-1\),所以第二组数不满足要求,舍去.
综上知,\(a=-\dfrac{11}{6}\)或\(a=\dfrac{3}{2}\sqrt{3}+1\).
在本题中,对分段函数的讨论是关键,因为\(a\)同时影响到分段函数的分界点和左半部分的解析式,所以直接讨论比较复杂,容易出现混乱.我们先不考虑分段点的情况,直接研究两段对应的函数的性质,得到一些确定的结论:\(4\)一定是\(f(x)=3\)的最大的根,从而将讨论的情况减少到只需讨论中间一个根是在左半段还是右半段,这就大大减少了需要讨论的情况,有助于条理清晰地讨论,得到结果.
更多零点相关的问题参见函数零点问题小结、每日一题[145]分段函数的零点、每日一题[281]零点分段讨论与分析端点、每日一题[293]零点问题的两种常见的思路.