解析几何问题的基本解题思路,就是借助点的坐标来表达条件,设直线的方程将坐标统一为横坐标或纵坐标,最后利用直线方程与椭圆方程的联立进行消参.但是,在实际的解题实践中,很多几何条件并不方便借助点的直角坐标来表达,此时恰当地引入极坐标处理问题会大幅简化运算.一般适用于极坐标表达的条件有:垂直、特殊三角形等等.
例1、利用极坐标表达垂直.
(2014年高考北京卷理科数学第19题)已知椭圆\(C:x^2+2y^2=4\).

(1)求椭圆\(C\)的离心率;
(2)设\(O\)为原点,若点\(A\)在椭圆\(C\)上,点\(B\)在直线\(y=2\)上,且\(OA\perp OB\),试判断直线\(AB\)与圆\(x^2+y^2=2\)的位置关系,并证明你的结论.
(1)解 \(e=\dfrac {\sqrt 2}2\);
(2)解 设\(A(\rho_A \cos\theta,\rho_A \sin\theta),B\left(\rho_B \cos\left(\theta+\dfrac {\pi}2\right),\rho_B \sin \left(\theta+\dfrac {\pi}2\right)\right)\)则\[\begin{split}\rho_A^2\cos^2\theta+2\rho_A^2\sin^2\theta&=4,\\\rho_B\sin\left(\theta+\dfrac {\pi}2\right)&=2.\end{split}\]从而\[\dfrac 1{\rho_A^2}=\dfrac 14\cos^2\theta+\dfrac 12\sin^2\theta,\dfrac 1{\rho_B^2}=\dfrac 14\cos^2\theta.\]而在\(\mathrm{Rt}\triangle OAB\)中,原点到直线\(AB\)的距离\(d\)满足\[\dfrac 1{d^2}=\dfrac 1{OA^2}+\dfrac 1{OB^2}=\dfrac 12.\]因此直线\(AB\)与圆\(x^2+y^2=2\)相切.
例2、利用极坐标表达特殊三角形.
(2014年北京东城二模)已知椭圆\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)的一个焦点为\(F(2,0)\),且离心率为\(\dfrac{\sqrt 6}3\).
(1)求椭圆方程;
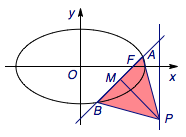
(2)斜率为\(k\)的直线\(l\)过点\(F\),且与椭圆交于\(A\)、\(B\)两点,\(P\)为直线\(x=3\)上的一点,若三角形\(ABP\)为等边三角形,求直线\(l\)的方程.
(1)解 椭圆方程为\[\dfrac{x^2}6+\dfrac{y^2}2=1.\]
(2)解 设直线\(AB\)的倾斜角为\(\theta\),线段\(AB\)的中点为\(M\).
由椭圆的极坐标方程得\[\begin{split}\overrightarrow{FA}&=\dfrac{2}{\sqrt 6+2\cos\theta}\left(\cos\theta,\sin\theta\right),\\\overrightarrow{FB}&=-\dfrac{2}{\sqrt 6-2\cos\theta}\left(\cos\theta,\sin\theta\right),\end{split}\]进而可得\[\overrightarrow{BA}=\overrightarrow{FA}-\overrightarrow{FB}=\dfrac{4\sqrt 6}{6-4\cos^2\theta}\left(\cos\theta,\sin\theta\right),\]于是\[\begin{split}\overrightarrow{MP}&=\dfrac{\sqrt 3}2\left|\overrightarrow{BA}\right|\left(\cos\left(\theta-\dfrac{\pi}2\right),\sin\left(\theta-\dfrac{\pi}2\right)\right)\\&=\dfrac{6\sqrt 2}{6-4\cos^2\theta}\left(\sin\theta,-\cos\theta\right).\qquad\cdots (*)\end{split}\]
另一方面,由中点坐标公式,有\[\overrightarrow{FM}=\dfrac 12\left(\overrightarrow{FA}+\overrightarrow{FB}\right)=\left(-\dfrac{4\cos^2\theta}{6-4\cos^2\theta},-\dfrac{4\cos\theta\sin\theta}{6-4\cos^2\theta}\right),\]因此\(M\)的横坐标为\[2-\dfrac{4\cos^2\theta}{6-4\cos^2\theta}.\qquad\cdots (**)\]
于是由(*)(**)有两种方式表达\(\overrightarrow{MP}\)的横坐标,可以得到方程\[3-\left(2-\dfrac{4\cos^2\theta}{6-4\cos^2\theta}\right)=\dfrac{6\sqrt 2}{6-4\cos^2\theta}\cdot\sin\theta,\]解得\[\sin\theta=\dfrac{\sqrt 2}2,\]进而可得直线\(l\)的方程为\[l:x=\pm y+2.\]
下面给出几道练习题.
练习1、(2014年北京丰台二模)已知椭圆\(E:\dfrac{x^2}8+\dfrac{y^2}4=1\)与直线\(l:y=kx+m\)交于\(A,B\)两点,\(O\)为坐标原点.
(1)若直线\(l\)过椭圆\(E\)的左焦点,且\(k=1\),求三角形\(AOB\)的面积;
(2)若\(OA\perp OB\),且直线\(l\)与圆\(O:x^2+y^2=r^2\)相切,求圆\(O\)的半径\(r\)的值.
练习2、双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(b>a>0)\),\(O\)为坐标原点,离心率\(e=2\),点\(M\left(\sqrt 5,\sqrt 3\right)\)在双曲线上.
(1)求双曲线的方程;
(2)若直线\(l\)与双曲线交于\(P\)、\(Q\)两点,且\(\overrightarrow{OP}\cdot\overrightarrow{OQ}=0\),求\(\dfrac{1}{OP^2}+\dfrac{1}{OQ^2}\)的值.
练习3、已知点\(P_1,P_2,\cdots,P_n\)为椭圆\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)上的\(n\)个点,且\(OP_1,OP_2,\cdots,OP_n\)将原点处的周角\(n\)等分.求证\[\dfrac{1}{OP_1^2}+\dfrac{1}{OP_2^2}+\cdots+\dfrac{1}{OP_n^2}\]为定值.
练习4、求抛物线\(y^2=2px(p>0)\)的内接等腰直角三角形面积的最小值.
练习5、在平面直角坐标系\(xOy\)中,直角三角形\(ABC\)的三个顶点都在椭圆\(\dfrac{x^2}{a^2}+y^2=1\)(\(a>0\))上,其中\(A(0,1)\)为直角顶点,若该三角形的面积的最大值为\(\dfrac{27}{8}\),求\(a\)的值.
参考答案:练习1、(1)\(8/3\);(2)\(\dfrac{2\sqrt 6}3\).
练习3、(1)\(\dfrac{x^2}{4}-\dfrac{y^2}{12}=1\);(2)定值为\(\dfrac{1}{a^2}-\dfrac{1}{b^2}=\dfrac 16\).
练习3、定值为\(\dfrac{n}{2}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\).
练习5、\(3\).