每日一题[1] 特殊三角形的极坐标表达

求抛物线$y^2=2px(p>0)$的内接等腰直角三角形面积的最小值．

---

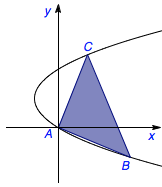
设抛物线的内接等腰直角三角形为$\triangle ABC$，直角顶点为$A(2pt^2,2pt)$，平移坐标系，使得原点为$A$，则抛物线方程变为

$$(y+2pt)^2=2p(x+2pt^2),$$

即

$$y^2+4pty-2px=0.$$

此时，可设$B(r\cos\theta,r\sin\theta)$，$C(-r\sin\theta,r\cos\theta)$，则

$$r^2\sin^2\theta+4pt\cdot r\sin\theta-2p\cdot r\cos\theta=0,\\r^2\cos^2\theta+4pt\cdot r\cos\theta+2p\cdot r\sin\theta=0.$$

于是

$$4t=\dfrac{2p\cos\theta-r\sin^2\theta}{p\sin\theta}=\dfrac{2p\sin\theta+r\cos^2\theta}{-p\cos\theta},$$

从而解得

$$r=\dfrac{2p}{\sin\theta\cdot\cos\theta(\sin\theta-\cos\theta)}.$$

其中，令$S=\sin\theta\cdot\cos\theta$，则由于$\theta\in\left(-\dfrac{\pi}2,0\right)$，于是$S\in\left[-\dfrac 12,0\right)$．

此时

$$S_{\triangle ABC}=\dfrac 12r^2=\dfrac{2p^2}{s^2(1-2s)},$$

于是当$s=-\dfrac 12$，即$\theta=-\dfrac{\pi}4$时，$\triangle ABC$的面积取得最小值为$4p^2$．

注    此题为2014年北京市海淀区查漏补缺题改编而成．

---

另法    设$A\left(\dfrac{a^2}{2p},a\right),B\left(\dfrac{b^2}{2p},b\right),C\left(\dfrac{c^2}{2p},c\right)$，则

$$\begin{split}S_{\triangle ABC}&=\dfrac 12AB^2\\&=\dfrac 12\left[(a-b)^2+(c-a)^2\right]\\&=\dfrac 12[2a^2-2a(b+c)+b^2+c^2].\end{split}$$

又$AC\perp AB$,于是

$$\dfrac{c-a}{\dfrac{c^2}{2p}-\dfrac{a^2}{2p}}\cdot\dfrac{b-a}{\dfrac{b^2}{2p}-\dfrac{a^2}{2p}}=-1,$$ 整理得 $$a(b+c)=-a^2-bc-4p^2,$$

代入面积的计算式可得

$$S_{\triangle ABC}=2a^2+\dfrac 12(b+c)^2+4p^2.$$

于是当$A(0,0),B(2p,2p),C(2p,-2p)$时，抛物线的内接等腰直角三角形面积最小，最小值为$4p^2$．