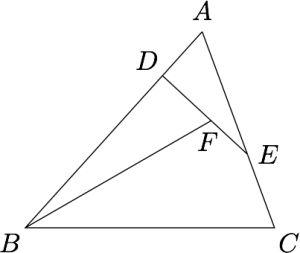
如图，已知$\triangle ABC$的面积为$2$，$D,E$分别为边$AB,AC$上的点，$F$为线段$DE$上一点，设$\dfrac{AD}{AB}=x,\dfrac{AE}{AC}=y,\dfrac{DF}{DE}=z,$ 且 $y+z-x=1$，则$\triangle BDF$面积的最大值为( )
A．$\dfrac{8}{{27}}$
B．$\dfrac{{10}}{{27}}$
C．$\dfrac{{14}}{{27}}$
D．$\dfrac{{16}}{{27}}$
12．几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案： 已知数列$1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,\cdots ,$其中第一项是$2^0$，接下来的两项是$2^0,2^1$，再接下来的三项是$2^0,2^1,2^2$，依此类推．求满足如下条件的最小整数$N$：$N>100$且该数列的前$N$项和为$2$的整数幂．那么该款软件的激活码是 ( )
A．$440$
B．$330$
C．$220$
D．$110$
如图，已知动直线$l$经过点$P\left( {4,0} \right)$，交抛物线${y^2} = 2ax$（$a > 0$）于$A$、$B$两点．坐标原点$O$是$PQ$的中点，设直线$AQ$、$BQ$的斜率分别为${k_{AQ}}$、${k_{BQ}}$．
(1)证明：${k_{AQ}} + {k_{BQ}} = 0$；
(2)当$a = 2$时，是否存在垂直于$x$轴的直线$l'$，被以$AP$为直径的圆截得的弦长为定值？若存在，请求出直线$l'$的方程；若不存在，请说明理由．
设函数$f\left( x \right)$是定义在${\mathbb{R}}$上的奇函数，且对任意的${x_1}, {x_2} \in \left[ {1 ,a} \right]$，当${x_2} > {x_1}$时，总有$f\left( {{x_2}} \right) > f\left( {{x_1}} \right) > 0$，则下列不等式一定成立的是__________（填上你认为正确的结论的序号）：
(1)$f\left( a \right) > f\left( 0 \right)$；
(2)$f\left( {\dfrac{{1 + a}}{2}} \right) > f\left( {\sqrt a } \right)$；
(3)$f\left( {\dfrac{{1 - 3a}}{{1 + a}}} \right) > f\left( { - 3} \right)$；
(4)$f\left( {\dfrac{{1 - 3a}}{{1 + a}}} \right) > f\left( { - a} \right)$．
已知$f(x) =\begin{cases}\lg \left( x + 1 \right) + 1 ,x \geqslant 0\\\lg \left( 1 - x \right) + 1 ,x < 0 \end{cases}$，若不等式$f\left( {ax - 1} \right) > f\left( {x - 2} \right)$在$\left[ {3,4} \right]$上有解，则实数$a$的取值范围为_________．
已知三棱锥$S - ABC$的底面$ABC$为正三角形，点$A$在侧面$SBC$上的射影$H$是$\triangle SBC$的垂心，二面角$H - AB - C$为$30^\circ $，且$SA = 2$，则此三棱锥的体积为( )
A．$\dfrac{1}{2}$
B．$\dfrac{{\sqrt 3 }}{2}$
C．$\dfrac{{\sqrt 3 }}{4}$
D．$\dfrac{3}{4}$
已知$a_1,a_2,\cdots,a_{10}$为大于零的正实数，且$${a_1} + {a_2} + \cdots + {a_{10}} = 30,{a_1}{a_2} \cdots {a_{10}} < 21,$$求证：$a_1,a_2,\cdots,a_{10}$中必有一个数在$(0,1)$之间．
1．求圆$\begin{cases}(x-4)^2+(y-7)^2+(z+1)^2=36,\\ 3x+y-z=9,\end{cases}$的圆心和半径．
从$O$点发出两条射线${l_1},{l_2}$，已知直线$l$分别交${l_1},{l_2}$于$A,B$两点，且${S_{\triangle OAB}} = c$（$c$为定值），记$AB$中点为$D$，$D$随着$A,B$的运动构成轨迹$\Gamma$．
求证：(1)$D$的轨迹$\Gamma$关于$\angle AOB$的角平分线反射对称；
(2)轨迹$\Gamma$为双曲线．
在$\triangle ABC$中，$AB = 2AC$，$AD$是$A$的角平分线，且$AD = kAC$.
(1) 求$k$的取值范围;
(2) 若${S_{\triangle ABC}} = 1$，问$k$为何值时，$BC$最短？
