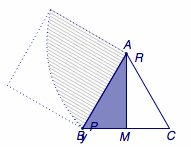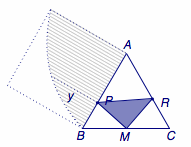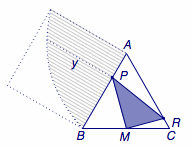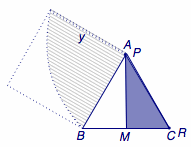
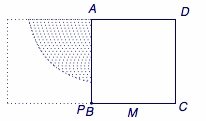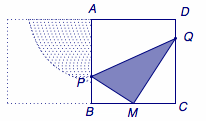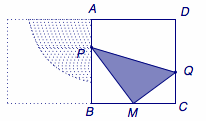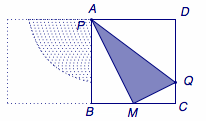
在正三角形\(ABC\)的底边\(BC\)上取中点\(M\),在与底边\(BC\)相邻的两条边\(BA\)和\(CA\)上分别取点\(P\)、\(Q\),若线段\(PQ\)对\(M\)的张角\(\angle PMQ\)为锐角,则称点\(P\)、\(Q\)亲密.若点\(P\)、\(Q\)在\(BA\)、\(CA\)上的位置随机均匀分布,则\(P\)、\(Q\)亲密的概率称为正三角形的亲密度.试求正三角形的亲密度.
正确答案是\(\dfrac {6-3\ln 3}{4}\),约为\(0.676\).
解 不妨设\(AB=BC=CA=2\),记\(BP=x\),\(0\leqslant x\leqslant 2\).
过\(M\)作\(PM\)的垂线,交\(AC\)于\(R\),则当\(Q\)落在线段\(AR\)内部及\(A\)点上时,\(P\)与\(Q\)是亲密的.记\(AR\)的长度为\(y=f(x)\).
由\[PM^2+MR^2=RP^2,\]及余弦定理得\[\left(x^2-x+1\right)+\left[(2-y)^2-(2-y)+1\right]=(2-x)^2-(2-x)y+y^2,\]整理得\[y=\dfrac{3x}{1+x},\]因此正三角形的亲密度为\[\dfrac 14\int_{0}^{2}\dfrac{3x}{1+x}{\mathrm d}x=\dfrac{6-3\ln 3}4.\]
接下来,直觉上我们知道正方形的亲密度一定比正三角形低,那么具体的数值是多少呢?留给读者作练习吧!
答案 \(\dfrac{3-2\ln 2}4\),约为\(0.403\).
注 有趣的是,我们很容易证明正三角形的亲密度大于\(0.5\),而正方形的亲密度小于\(0.5\).