椭圆的“姊妹圆”

椭圆有两个重要的伴随轨迹，它们是以椭圆的中心为圆心的同心圆，我们称之为椭圆的“姊妹圆”．以这两个圆为背景的试题在各类考试中屡见不鲜，下面我们来看看这两个圆的形成过程以及性质．

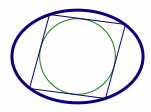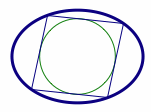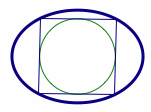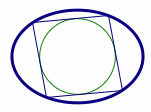
如图，对于任意椭圆 $$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,$$ 都存在圆 $$C_1:x^2+y^2=R^2,R^2=a^2+b^2,$$ 从圆$C_1$上任意一点对椭圆的切点弦的张角恒为直角．

如图，对于任意椭圆 $$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,$$ 都存在圆 $$C_2:x^2+y^2=r^2,\dfrac 1{r^2}=\dfrac 1{a^2}+\dfrac 1{b^2},$$ 从圆$C_2$的任意切线被椭圆截得的弦对椭圆中心的张角恒为直角．

事实上，由于抛物线类似的性质对应的交点轨迹为抛物线的准线，因此我们又把半径满足$R^2=a^2+b^2$的圆称为椭圆的“准圆”．在解析几何发展史上，这个圆也大有来头，称之为“蒙日圆”．

想想看，双曲线是否也有对偶的性质呢？

例如，2014年北京高三模拟考试中的两道解析几何试题就是以姊妹圆为背景命题的．

（石景山区一模）给定椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$,称圆心在原点$O$，半径为$\sqrt{a^2+b^2}$的圆是椭圆$C$的“准圆”．若椭圆$C$的一个焦点为$F(\sqrt 2,0)$，其短轴上的一个端点到$F$的距离为$\sqrt 3$．

（1）求椭圆$C$的方程和其“准圆”的方程；

（2）点$P$是椭圆$C$的“准圆”上的动点，过点$P$作椭圆的切线$l_1$，$l_2$交“准圆”于点$M$，$N$．

① 当$P$为“准圆”与$y$轴正半轴的交点时，求直线$l_1$，$l_2$的方程并证明$l_1\perp l_2$；

② 求证：线段$MN$的长为定值．

（丰台区二模）已知椭圆$E:\dfrac{x^2}8+\dfrac{y^2}4=1$与直线$l:y=kx+m$交于$A$，$B$两点，$O$为坐标原点．

（1）若直线$l$过椭圆$E$的左焦点，且$k=1$，求$\triangle AOB$的面积；

（2）若$OA\perp OB$，且直线$l$与圆$O:x^2+y^2=r^2$相切，求圆$O$的半径$r$的值．

注     事实上，以椭圆的“姊妹圆”为背景的题在往年高考题中也很多，比如2009年北京卷理科数学解析几何大题，2014年广东卷理科数学解析几何大题．

2015年10月10日补充椭圆准圆的一条优美性质：

椭圆上的任意一点到两个焦点的距离之积等于该点到通过该点的准圆直径的两个端点的距离之积．