每日一题[136] 平面向量上的“攻守战”

2013年高考广东卷文科数学第10题（选择压轴题）：

设$\overrightarrow a$是已知的平面向量且$\overrightarrow a\neq \overrightarrow 0$，关于向量$\overrightarrow a$的分解，有如下四个命题：

①  给定向量$\overrightarrow b$，总存在向量$\overrightarrow c$，使$\overrightarrow a=\overrightarrow b +\overrightarrow c$；

②  给定向量$\overrightarrow b$和$\overrightarrow c$，总存在实数$\lambda$和$\mu$，使$\overrightarrow a=\lambda\overrightarrow b+ \mu \overrightarrow c$；

③  给定单位向量$\overrightarrow b$和正数$\mu$，总存在单位向量$\overrightarrow c$和实数$\lambda$，使$\overrightarrow a=\lambda \overrightarrow b+\mu \overrightarrow c$；

④  给定正数$\lambda$和$\mu$，总存在单位向量$\overrightarrow b$和单位向量$\overrightarrow c$，使$\overrightarrow a=\lambda \overrightarrow b+\mu \overrightarrow c$．

上述命题中的向量$\overrightarrow b$、$\overrightarrow c$和$\overrightarrow a$在同一平面内且两两不共线，则真命题的个数是（        ）

A．1

B．2

C．3

D．4

正确答案是B．

真命题为①②．

对于这类同时包含全称量词和特称量词的命题，我们可以利用“攻守战”来理解．在本题中，作战的大环境为已知非零向量$\overrightarrow a$，双方作战的基本规则为保证向量$\overrightarrow a$、向量$\overrightarrow b$、向量$\overrightarrow c$在同一个平面内，且两两不共线．在每个命题中 “进攻方”与“防守方”都拥有一定的资源，比如在命题①中，“进攻方”掌握的资源为$\overrightarrow b$，而作为“防守方”，掌握的资源为$\overrightarrow c$．我们需要同时扮演双方，并且推断出在双方都足够聪明的情况下，哪一方有必胜的策略．

①  “防守方”必胜．

对任意的向量$\overrightarrow b$，取$\overrightarrow c=\overrightarrow a-\overrightarrow b$．考虑到$\overrightarrow b$与$\overrightarrow a$不共线，于是显然有$\overrightarrow c$既不与$\overrightarrow a$共线，也不与$\overrightarrow b$共线，符合题设．此时就有  $\overrightarrow a= \overrightarrow b+\overrightarrow c$成立，“防守方”稳操胜券，因此命题①正确．

②  “防守方”必胜

对任意给定的不共线向量$\overrightarrow b$和$\overrightarrow c$，它们构成平面的一组基底．因此根据平面向量分解的基本定理，平面上的任意向量（包括且不限于向量$\overrightarrow a$）都可以由向量$\overrightarrow b$和$\overrightarrow c$唯一线性表示，“防守方”防守得无懈可击，因此命题②正确．

③  “进攻方”必胜

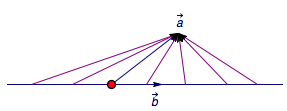
作为“进攻方”，我们首先给出与向量$\overrightarrow a$不共线的向量$\overrightarrow b$．考虑到“防守方”握有实数$\lambda$，因此$\lambda \overrightarrow b$可以遍布向量$\overrightarrow b$所在的整条基线．此时考虑“防守方”为了达到目的，就要使得$\mu \overrightarrow c=\overrightarrow a-\lambda\overrightarrow b$．$\overrightarrow a-\lambda \overrightarrow b$有无数种可能，如图．

此时“进攻方”还拥有一张王牌——实数$\mu$，我们发现“防守方”的重要资源之一向量$\overrightarrow c$有致命缺陷——长度为$1$，于是可以采用以下策略保证“进攻方”必胜：令$\mu$为向量$\overrightarrow a$的终点到向量$\overrightarrow b$的基线距离的一半，则向量$\mu \overrightarrow c$会受到长度的限制而无法成为无数个向量$\overrightarrow a-\lambda \overrightarrow b$中的任何一个，因此命题③错误．

④  “进攻方”必胜

有了③的经验，这次“进攻方”的获胜要简单很多．由于“防守方”的资源——向量$\overrightarrow b$和向量$\overrightarrow c$的长度均被限制为$1$，于是可以令$\lambda=\mu=\dfrac 13\left|\overrightarrow a\right|$，则无论如何向量$\lambda \overrightarrow b+\mu \overrightarrow c$的长度不超过$\dfrac 23\left|\overrightarrow a\right|$，因此等式$\overrightarrow a=\lambda \overrightarrow b+\mu \overrightarrow c$无法成立，“进攻方”轻松获胜，因此命题④错误．

综上，只有命题①②为真命题，正确答案为B．