在正方形\(ABCD\)的外侧作直线\(AP\)，点\(B\)关于直线\(AP\)的对称点为\(E\)，连接\(BE，DE\)，其中\(DE\)交直线\(AP\)于点\(F\)．若\(45^\circ<\angle PAB<90^\circ\)，则\(AB，EF，FD\)存在怎样的等量关系？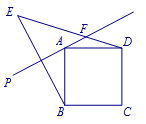
分析 求三条分散的线段关系，一般要将线段集中在一个三角形中或一条直线上，因为已知中有对称点，所以我们可以通过对称去转移线段．
解
连接\(BF，BD\)．根据对称的性质可得\[EF=FB,\]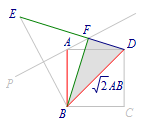
因为\(BD=\sqrt 2 AB\)，所以将\(AB，EF，FD\)三条线段转移到了\(\triangle FBD\)中．
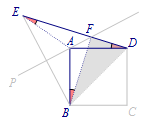连接\(AE\)，则\[\angle AED=\angle ADE=\angle ABF,\]所以\[\angle BAD=\angle BFD=90^\circ,\]所以\[EF^2+FD^2=BD^2=2AB^2.\]
练习 在等边三角形\(ABC\)外侧作直线\(AP\)，点\(B\)关于直线\(AP\)的对称点为\(D\)，连接\(BD，CD\)，其中\(CD\)交直线\(AP\)于点\(E\)．若\(60^\circ<\angle PAB<120^\circ\)，证明由线段\(AB、CE、DE\)可以构成一个含有\(60^\circ\)角的三角形．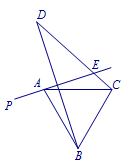
解
连接 \(AD\)，\(BE\)，根据对称的性质，将\(DE\)，\(AB\)，\(EC\)转移到\(\triangle BEC\)中，
则\(\angle ADC=\angle ACD=\angle ABE\)，所以\(\angle BEC=\angle BAC=60^\circ\)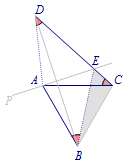
所以线段\(AB、CE、DE\)可以构成一个含有\(60^\circ\)角的三角形．
