等边三角形——牵线搭桥我最行

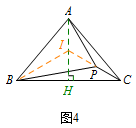
等腰三角形内一点与三顶点连线组成的图形问题，通常以等腰三角形的一条边向同侧作等边三角形，从而得到更多的边等角等（如图1~3）；当然有时也能由等腰三角形的对称性来解决问题（如图4）．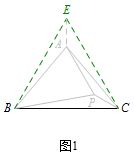

注　《条条大路通罗马》中所给的例题和练习题比较特殊，并不是每题都所有方法皆可，“边边”有缘，总有一款可行．

---

例1　如图，在$\triangle ABC$中，$AB=AC$，$P$为$\triangle ABC$内一点，连接$PA,PB,PC$，且$\angle BAP=70^\circ$，$\angle ABP=40^\circ$，$\angle PCB=30^\circ$，求$\angle PBC$的度数．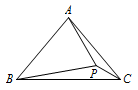

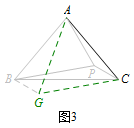
解　如图，以$BC$为边在$\triangle ABC$同侧作等边$\triangle BCE$，连接$AE$．若$\triangle BAE \cong \triangle BPC$，即可求得$\angle PBC$的度数．但由已知条件$\mathrm{SSA}$不能证明全等，而要求的是角，所以只能通过$\mathrm{SSS}$来证全等．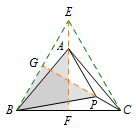
延长$EA,CP$，分别与等边$\triangle BCE$的边交于点$F,G$．则

$$\mathrm{Rt}\triangle ABF\cong \mathrm{Rt}\triangle PGB\ (\mathrm{HL}).$$ 所以 $$AF=PG,EA=CP.$$ 从而$\triangle BAE \cong \triangle BPC$得证，故 $$\angle PBC=\angle ABE=10^\circ.$$

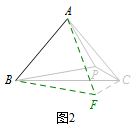
例2　如图，在$\triangle ABC$中，$AB=AC$，$\angle BAC=80^\circ$，$D$为形内一点，且$\angle DAB=\angle DBA=10^\circ$，求$\angle ACD$的度数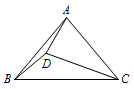．解　如图，以$AC$为边在$\triangle ABC$同侧作等边$\triangle ACE$，连接$BE,DE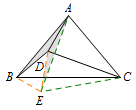$．易证

$$\triangle ADB\cong \triangle ADE\ (\mathrm{SAS}),$$ 所以 $$DE=DB=DA.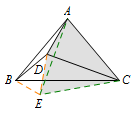$$ 从而证得 $$\triangle ACD\cong \triangle ECD\ (\mathrm{SSS}),$$ 所以 $$\triangle ACD=\angle ECD=30^\circ.$$

---

练习　如图，在$\triangle ABC$中，$AB=AC=8$，$\angle BAC=80^\circ$，$P$为$\triangle ABC$内一点，且$\angle PBC=10^\circ$，$\angle PCB=30^\circ$．求$PB$的长．答案　$PB=8$．