2015年安徽省中考数学第23（3）题：
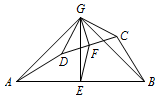
如图，在四边形\(ABCD\)中，点\(E,F\)分别是\(AB,CD\)的中点，过点\(E\)作\(AB\)的垂线，过点\(F\)作\(CD\)的垂线，两垂线交于点\(G\)，连接\(AG,BG,CG,DG\)，且\(\angle AGD=\angle BGC\)．若\(AD,BC\)所在的直线互相垂直，求\(\dfrac {AD}{EF}\)．
证明与解 由题意可得\(\triangle AGB\)和\(\triangle DGC\)为共顶点等顶角的两个等腰三角形，这是初中平面几何中常见的“手拉手模型”，易证\[\triangle AGD \cong \triangle BGC,\triangle AGD \sim \triangle EGF.\]\(AD,BC\)为不相交且互相垂直的两条线段，一般通过延长或平移线段得直角．
方法一 利用中点中线倍长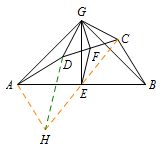
连接\(CE\)并延长至点\(H\)，使得\(EH=EC\)，连接\(AH\)．则\[AH \parallel BC,AH=BC.\]连接\(DH\)，则\(\triangle ADH\)为等腰直角三角形．
而点\(E,F\)为\(CH,CD\)的中点，所以\[\dfrac {AD}{EF}=\dfrac {AD}{\dfrac 12 DH}=\sqrt 2.\]
方法二 利用中点构造中位线
四边形，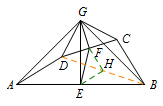
如图，连接\(BD\)并取中点\(H\)，连接\(EH,FH\)，则\(\triangle EHF\)为等腰直角三角形．
所以\[\dfrac {AD}{EF}=\dfrac {2EH}{EF}=\sqrt 2.\]
注 若四边形一组对边相等，另一组对边给中点，则连对角线取中点得等腰三角形．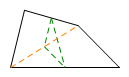
方法三 延长线段得直角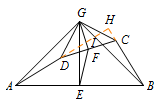
延长\(AD,BC\)交于点\(H\)，与\(BG\)交于点\(I\)，则\(\angle AHB=90^\circ\)．
已证\(\triangle AGD \cong \triangle BGC\)，得\(\angle GAI=\angle HBI\)，所以\[\angle AGI =\angle BHI=90^\circ.\]由\(\triangle AGD \sim \triangle EGF\)，可得\[\dfrac {AD}{EF}=\dfrac {AG}{EG}=\sqrt 2.\]
更多“中点”问题请阅读：《小小的点儿，大大的能量》