练习题[27] 来几个题目先精选（一）

题目精选自高中数学吧  来几个题目先．

1、（269楼问题）设\(m\)和\(n\)是两条异面直线，过直线\(m\)上等距三点\(A\)、\(B\)、\(C\)作直线\(n\)的垂线，垂足分别为\(A'\)、\(B'\)、\(C'\)，若\(AA'=\sqrt{15}\)，\(BB'=\dfrac 72\)，\(CC'=\sqrt{10}\)，则直线\(m\)与\(n\)的距离为_______．

2、（270楼问题）已知\(A\)、\(B\)、\(C\)为任意实数，则\(\sin^2A\cos^2B+\sin^2B\cos^2C+\sin^2C\cos^2A\)的最大值为_______．

3、（282楼问题）已知\(\overrightarrow a\)、\(\overrightarrow b\)满足\(\left|\overrightarrow a\right|=1\)，\(\langle \overrightarrow b,\overrightarrow b-\overrightarrow a\rangle =120^\circ\)，则\(\left|\overrightarrow b\right|^2-\left(\overrightarrow a\cdot \overrightarrow b\right)^2\)的最大值为_______．

4、（282楼问题）解不等式：\(x^{12}+3x^{10}+5x^8+3x^6-2x^4-1\leqslant 0\)．

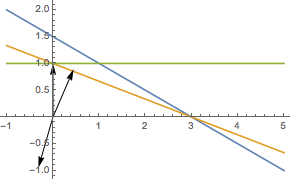
5、（290楼问题）已知变量\(x,y\)满足约束条件\(\begin{cases}x+2y-3\leqslant 0,\\x+3y-3\geqslant 0,\\y-1\leqslant 0.\end{cases}\)若目标函数\(z=ax+by\)（\(a\neq 0\)）取得最大值时的最优解有无数多组，求点\((a,b)\)的轨迹．

6 、（238楼问题）\(P,Q\)是两个定点，点\(M\)为平面内的动点，且\(\dfrac{MP}{MQ}=\lambda\)（\(\lambda >0\land \lambda \neq 0\)）．点\(M\)的轨迹围成的平面区域的面积为\(S(\lambda)\)，判断\(S(\lambda)\)的单调性．

7、（251楼问题）已知定义在同一个区间\(\left(\dfrac{\sqrt 3}3,\dfrac{\sqrt 6}2\right)\)的两个函数\(f(x)=x^2-2a\ln x\)，\(g(x)=x^3-bx^2+x\)在\(x=x_0\)处的切线均平行于\(x\)轴．

（1）求实数\(a\)与实数\(b\)的取值范围；

（2）试问：是否存在实数\(x_1,x_2\)，当\(x_1,x_0,x_2\)成等比数列时，等式\(f\left(x_1\right)+f\left(x_2\right)=2g\left(x_0\right)\)成立？若成立，求出实数\(a\)的取值范围；若不存在，请说明理由．

---

参考答案

1、\(\sqrt 6\)

2、\(1\)

提示    记\(a=\sin^2A\)，\(b=\sin^2 B\)，\(C=\sin^2C\)，则原式为\(\sum\limits_{cyc}a(1-b)\)，该式对\(a,b,c\)而言均为一次函数，于是最大值点在边界处取得．事实上，当\((a,b,c)=(0,0,1),(0,1,1)\)时原式取得最大值为\(1\)．

3、\(\dfrac 34\)

提示    如图，\(OA=1\)，优弧\(OA\)所对的圆周角为\(120^\circ\)，\(B\)在劣弧\(OA\)上运动，欲求几何量为\(B\)到\(OA\)距离的平方．

4、\(\left[-\sqrt{\dfrac{\sqrt 5-1}{2}},\sqrt{\dfrac{\sqrt 5-1}{2}}\right]\)

提示    原不等式即\[\left(x^2+1\right)^3+2x^2\leqslant \left(\dfrac{1}{x^2}\right)^3+2\cdot\dfrac{2}{x^2},\]即\[x^2+1\leqslant \dfrac 1{x^2}.\]

5、如图，注意去掉原点．

6、\(S(\lambda)\)在\((0,1)\)上单调递增，在\((1,+\infty)\)上单调递减．

提示    \(M\)的轨迹为圆，且\[S(\lambda)=\pi a^2\cdot\dfrac{\lambda^2}{\left(1-\lambda^2\right)^2}.\]

7、（1）\(a\)的取值范围是\(\left(\dfrac 13,\dfrac 32\right)\)，\(b\)的取值范围是\(\left(\sqrt 3,\dfrac{11\sqrt 6}{12}\right)\)．（2）不存在．

提示    （2）由（1）可得\[a=x_0^2,b=\dfrac 12\left(3\sqrt a+\dfrac{1}{\sqrt a}\right),\]于是\[\begin{split}f\left(x_1\right)+f\left(x_2\right)&=\left(x_1-x_2\right)^2-2a\ln a+2a,\\2g\left(x_0\right)&=-a\sqrt a+\sqrt a,\end{split}\]构造函数\[h(a)=f\left(x_1\right)+f\left(x_2\right)-2g\left(x_0\right),\]该函数为单调递增函数，且\(h\left(\dfrac 13\right)>0\)，于是不存在符合题意的\(a\)．