练习题集[82]基础练习

1．求图中阴影部分的面积(单位：${\rm cm}$)

2．若$a,b,c\geqslant 0$，且$a^2+b^2+c^2=1$，则$a+b+\dfrac 12\sqrt{4c^2+\left(a^2-b^2\right)^2}$的最大值为_______．

3．已知$a,b,c\geqslant 0$，且满足$ab+bc+ca=a+b+c>0$，则$\sqrt{ab}+\sqrt{bc}+\sqrt{ca}$的最小值为______．

4．求$\displaystyle \sum_{i=1}^{\infty}\arctan\dfrac{1}{2i^2}$．

5．证明：
(1) ${\rm e}<1+\sqrt 3$；
(2) $\dfrac{1}{\sqrt 7}+\dfrac{1}{\sqrt 8}<\dfrac{2}{\rm e}$．

6．给定$n$个正整数，考虑由这$n$个正整数中的一个或多个相加得到的所有的和．求证：这些和可以分成$n$组，且每一组中最大数与最小数之比不大于$2$．

7．已知$x>0$，求证：${\rm e}^x-x^2-2x+2>0$．

---

参考答案

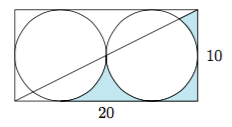
1．$90+25\arctan 2-\dfrac{125\pi}4$．

提示　右上角的弧所对的圆心角为$\arctan\dfrac 43=\pi-2\arctan 2$．

2．$\sqrt 3$．

令$a+b=x$，$a-b=y$，则 $$\begin{split} a+b+\dfrac 12\sqrt{4c^2+\left(a^2-b^2\right)^2}&=x+\dfrac 12\sqrt{4-2x^2-2y^2+x^2y^2}\\&=x+\dfrac 12\sqrt{\left(2-x^2\right)\left(2-y^2\right)}\\&\leqslant x+\dfrac{\sqrt{4-2x^2}}2\\&\leqslant \sqrt{\dfrac 12+\dfrac 14}\cdot \sqrt{2x^2+4-2x^2}\\&=\sqrt 3,\end{split}$$ 等号当$a=b=c=\dfrac{1}{\sqrt 3}$时取得．因此所求的最大值为$\sqrt 3$．

3．$2$．

不妨设$a\geqslant b\geqslant c$，根据题意，有 $$\begin{split} \sqrt{ab}+\sqrt{bc}+\sqrt{ca}&=\dfrac{\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\left(a+b+c\right)}{ab+bc+ca}\\ &\geqslant \dfrac{\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\cdot 2\sqrt{ab}}{ab+bc+ca}\\ &\geqslant 2,\end{split}$$ 等号当$a=b=2$，$c=0$时取得．因此所求的最小值为$2$．

4．由于 $$\arctan\dfrac{1}{2i^2}=\arctan\dfrac{(2i+1)-(2i-1)}{1+(2i+1)(2i-1)}=\arctan(2i+1)-\arctan(2i-1),$$ 于是 $$\begin{split} \sum_{i=1}^{\infty}\arctan\dfrac{1}{2i^2}&=\lim_{n\to \infty}\sum_{i=1}^{n}\left[\arctan (2i+1)-\arctan (2i-1)\right]\\&=\lim_{n\to \infty}\left[\arctan (2n+1)-\arctan 1\right]\\&=\lim_{n\to \infty}\arctan\dfrac{2n}{2n+2}\\&=\dfrac{\pi}4.\end{split}$$

5．(1)对数估算　我们熟知 $$\ln\dfrac{1+x}{1-x}>2\left(x+\dfrac{x^3}3+\dfrac{x^5}5\right),$$ 于是令$x=2\sqrt 3-3$，就有 $$\begin{split} \ln \left(1+\sqrt 3\right)&>2\left[(2\sqrt 3 -3)+\dfrac 13((2\sqrt 3-3))^3+\dfrac 15(2\sqrt 3-3)^5\right]\\&=\dfrac 25\left(-5883+3398\sqrt 3\right)\\&>1,\end{split}$$ 于是不等式得证．

其他思路　利用${\rm e}<\left(1+\dfrac 1n\right)^{n+1}$，二项式展开后放缩．

(2)利用均值不等式，有
$$\begin{split} \dfrac{2}{\dfrac{1}{\sqrt 7}+\dfrac{1}{\sqrt 8}}&>\sqrt{\dfrac{2}{\dfrac 17+\dfrac 18}}=\sqrt{\dfrac{112}{15}}=\sqrt{4+2\cdot\sqrt{\dfrac{676}{225}}}\\&>\sqrt{4+2\sqrt 3}=1+\sqrt 3>{\rm e},\end{split}$$ 于是不等式得证．

6．对$n$进行归纳，$n=1$时显然．

假设$n<m$时结论都成立，考虑$n=m$的情况．

不妨设给定的正整数为$a_1\leqslant a_2\leqslant \cdots \leqslant a_m$，并令 $$S_i=a_1+a_2+\cdots +a_i,$$ 其中$1\leqslant i\leqslant m$．设$k\in \{1,2,\cdots ,m-1\}$是最大的满足$2S_k\leqslant S_{k+1}$的正整数(由$2S_1=2a_1\leqslant a_1+a_2=S_2$知这样的$k$存在)，则 $$a_{k+1}=S_{k+1}-S_k\geqslant \dfrac 12S_{k+1}\geqslant \dfrac 14S_{k+2}\geqslant \cdots \geqslant \dfrac{1}{2^{m-k}}S_m,$$ 及$S_m\leqslant 2^{m-k}a_{k+1}$，因此$m-k$个区间 $$\left[a_{k+1},2a_{k+1}\right),\left[2a_{k+1},4a_{k+1}\right),\cdots ,\left[2^{m-k-1}{a_{k+1}},2^{m-k}a_{k+1}\right]$$ 即可包含所有至少含$a_{k+1},a_{k+2},\cdots ,a_m$之一的一个或多个相加的和，再由归纳假设，$a_1,a_2,\cdots ,a_k$中一个或多个的和均可被分成$k$组，故一共可以分为$m$组，即结论对$n=m$也成立，证毕．

7．设$f(x)={\rm e}^x-x^2-2x+2$，则 $$f'(x)={\rm e}^x-2x-2,$$ 于是函数$f(x)$在$(0,1)$上单调递减，在$(2,+\infty)$上单调递增．结合 $$f(1)={\rm e}-1>0,f(2)={\rm e}^2-6>0,$$ 可得命题对$x\in (0,1)$和$x\in (2,+\infty)$成立．

接下来证明命题在$x\in (1,2)$时也成立．容易证明当$x\in (1,2)$时，有 $${\rm e}^x>\dfrac 12{\rm e}(x-1)^2+{\rm e}(x-1)+{\rm e}.$$ 接下来证明在区间$(1,2)$上，有 $$\dfrac 12{\rm e}(x-1)^2+{\rm e}(x-1)+{\rm e}>x^2+2x-2,$$ 即 $$({\rm e}-2)x^2-4x+{\rm e}+4>0,$$ 其判别式 $$\Delta=16-4({\rm e}-2)({\rm e}+4)<0,$$ 因此命题得证．

综上，原命题成立．