1．已知$f(x)$是四次多项式，且满足$f(k)=\dfrac 1k$，其中$k=1,2,3,4,5$，求$f(6)$的值．
2．在任意梯形中，一条与上下底均有交点的直线将梯形分割为面积相等的两个部分，求证：这条直线过定点．
3．(2013年北京市朝阳区二模)点$P$是棱长为$1$的正方体$ABCD-A_1B_1C_1D_1$的底面$A_1B_1C_1D_1$上一点，则$\overrightarrow {PA}\cdot \overrightarrow {PC_1}$的取值范围是______．
4．已知$\triangle ABC$内一点$D$满足$\angle BAD=\angle BCD$，且$\angle BDC=90^\circ$．已知$AB=5$，$BC=6$，$M$为$AC$中点，求$DM$．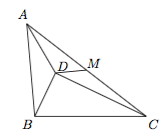
5．桌上放着一堆共计$40$枚棋子，甲乙两人轮流进行操作，每次操作均需要把所有棋子数大于$1$的堆分成两个较小的堆，规定谁能率先把所有棋子分成$40$堆谁就获胜．如果甲先操作，是否有必胜策略？如果有，请给出必胜策略；如果没有，请说明理由．
6．已知$n,k\in\mathcal N^*$，求证：$$\dfrac{n^{k+1}}{k+1}<1^k+2^k+\cdots+n^k<\left(1+\dfrac 1n\right)^k\cdot \dfrac{n^{k+1}}{k+1}.$$
7．已知$a,b,c>0$，求证：$\dfrac{a^3}{a^2-ab+b^2}+\dfrac{b^3}{b^2-bc+c^2}+\dfrac{c^3}{c^2-ca+a^2}<\dfrac 54(a+b+c)$．
参考答案
1．根据题意，$x=1,2,3,4,5$是关于$x$的五次方程$xf(x)-1=0$的根，因此$$xf(x)-1=\dfrac{(x-1)(x-2)(x-3)(x-4)(x-5)}{5!},$$进而$6f(6)-1=1$，从而$f(6)=\dfrac 13$．
2．如图，设$A(a,0),B(b,0),C(c,h),D(d,h),E(e,0),F(f,h)$且$a\leqslant e\leqslant b,d\leqslant f\leqslant c$．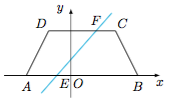
根据题意，梯形$AEFD$和梯形$CFEB$的面积相等，因此$$e+f=\dfrac 12(a+b+c+d),$$而直线$EF$的方程为$$y=\dfrac{h}{f-e}(x-e),$$即$$y=\dfrac{h}{\dfrac 12(a+b+c+d)-2e}(x-e),$$因此直线$E$恒过定点$\left(\dfrac{a+b+c+d}4,\dfrac h2\right)$．
4．根据极化恒等式，有$$\overrightarrow {PA}\cdot \overrightarrow {PC_1}=|OP|^2-\dfrac 14|AC_1|^2=|OP|^2-\dfrac 34,$$其中$O$为正方体的中心．因此所求的取值范围是$\left[-\dfrac 12,0\right]$．
5．作$\triangle BDC$的外接圆，并将$\triangle BDC$连同外接圆一起关于$BD$对称，设$C$的对应点为$C'$．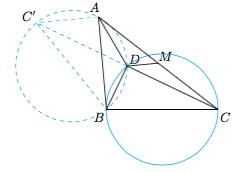
由于$\angle BAD=\angle BCD$，于是$A$点对称圆上且$D$为$CC'$的中点．于是$$DM=\dfrac 12AC'=\dfrac 12\sqrt{BC'^2-AB^2}=\dfrac 12\sqrt{BC^2-AB^2}=\dfrac {\sqrt {11}}2.$$6．考虑操作后留给对方的包含最多棋子的堆．甲要胜利必须拆出$3$，要拆出$3$就需要拆出$7$，依次类推，需要拆出$15,31$．因此甲只要先将$40$分为$31+9$，这样无论乙如何分割，必然会出现不小于$16$的堆，此时甲就可以顺利的拿到$15$，$\cdots $，最终获得胜利．
6．由于函数$f(x)=x^k$单调递增，考虑区间$[0,1]$上的分割$$0,\dfrac 1n,\dfrac 2n,\cdots ,\dfrac {n-1}n,1,$$可得$$\sum_{i=1}^{n}\left[\dfrac 1n\cdot \left(\dfrac{i}{n}\right)^k\right]>\int_0^1x^k{\ \rm d}x=\dfrac{1}{k+1}.$$而考虑分割$$\dfrac 1{n+1},\dfrac 2{n+1},\cdots ,\dfrac {n}{n+1},1,$$可得$$\sum_{i=1}^{n}\left[\dfrac 1n\cdot \left(\dfrac{i}{n+1}\right)^k\right]<\int_0^1x^k{\ \rm d}x=\dfrac{1}{k+1}.$$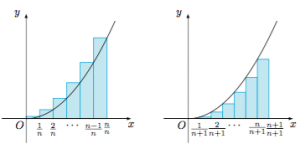
7．不妨设$a$为最大数，则\[\begin{split}\dfrac{a^3}{a^2-ab+b^2}=&a+\dfrac{ab(a-b)}{a^2-ab+b^2}\\<&a+\dfrac{ab(a-b)(a+b)}{a^3+b^3}\\\leqslant&a+\dfrac{a(a+b)}{a^3+b^3}\cdot\left(\dfrac{b+a-b}{2}\right)^2\\=&a+\dfrac{a+b}{4}\cdot\dfrac{a^3}{a^3+b^3}<\dfrac{5a+b}4,\end{split}\]而$$\dfrac{b^3}{b^2-bc+c^2}+\dfrac{c^3}{c^2-ca+a^2}<\dfrac{b^3+c^3}{b^2-bc+c^2}=b+c,$$于是$$\dfrac{a^3}{a^2-ab+b^2}+\dfrac{b^3}{b^2-bc+c^2}+\dfrac{c^3}{c^2-ca+a^2}<\dfrac{5a+b}4+b+c<\dfrac 54(a+b+c).$$