1．平面直角坐标系$xOy$中有两定点$P(x_1,y_1)$，$Q(x_2,y_2)$，分别过点$P$和点$Q$作直线$l_1,l_2$，且$l_1\perp l_2$，若直线$l_1$交$x$轴于点$A$，直线$l_2$交$y$轴于点$B$，求线段$AB$中点$M$的轨迹．
2．设$n$为自然数，$a,b$为正实数，且$a+b=2$，则$\dfrac{1}{1+a^n}+\dfrac{1}{1+b^n}$的最小值为________．
3．已知数列$\{a_n\},\{b_n\}$满足$a_0=1$，$b_0=0$，且$$\begin{cases} a_{n+1}=7a_n+6b_n-3,\\ b_{n+1}=8a_n+7b_n-4,\end{cases} $$其中$n=0,1,2,\cdots $．求证：$a_n$是完全平方数．
4．试比较${\rm e},\sqrt 3+1,\sqrt 7,\sqrt 8$的大小，并证明．
5．若方程$m\left(x^2+y^2+2y+1\right)=\left(x-2y+3\right)^2$表示的曲线是椭圆，求$m$的取值范围．
6．已知$x,y,z\geqslant 0$，且$x+y+z=6$，求$\sqrt{x^2+4}+\sqrt{y^2+9}+\sqrt{z^2+16}$的取值范围．
7．已知$n\in\mathcal N^*$，求证：$\left[\sqrt{n}+\sqrt{n+1}+\sqrt{n+2}\ \right]=\left[\sqrt{9n+8}\ \right]$．
参考答案
1．如图．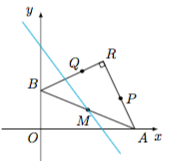
设$M(x,y)$，则$A(2x,0)$，$B(0,2y)$，于是由$\overrightarrow {AP}\cdot \overrightarrow {BQ}=0$，可得$$(x_1-2x,y_1)\cdot (x_2,y_2-2y)=x_1x_2-2x_2x+y_1y_2-2y_1y=0,$$因此所求的轨迹是直线，其方程为$2x_2x+2y_1y-x_1x_2-y_1y_2=0$．
2．原式即$$\dfrac{1+a^n+1+b^n}{(1+a^n)(1+b^n)}=1+\dfrac{1-(ab)^n}{1+a^n+b^n+a^nb^n}\geqslant 1,$$等号当$a=b=1$时取得，因此原式最小值为$1$．
3．消去$b_n$，可得$$a_{n+1}=15a_n-15a_{n-1}+a_{n-2},$$其特征方程为$$x^3=15x^2-15x+1,$$特征根为$x=1,7+4\sqrt 3,7-4\sqrt 3$，因此可得$$a_n=\dfrac 14\left[2+(7+4\sqrt 3)^n+(7-4\sqrt 3)^n\right]=\left[\dfrac{(2+\sqrt 3)^n+(2-\sqrt 3)^n}2\right]^2,$$因此$a_n$为完全平方数．
注意$\dfrac{(2+\sqrt 3)^n+(2-\sqrt 3)^n}2\in\mathcal{Z}$．
4．显然有$\sqrt 7<\sqrt 3+1<\sqrt 8$，接下来证明$\sqrt 7<{\rm e}<\sqrt 3+1$．
考虑到$${\rm e}=1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\cdots +\dfrac{1}{n!}+\cdots ,$$于是$${\rm e}>1+1+\dfrac 12+\dfrac 16=\dfrac {8}3,$$因此${\rm e}^2>\dfrac{64}{9}>7$，即${\rm e}>\sqrt 7$．
又\[\begin{split} {\rm e}&<1+1+\dfrac 12+\dfrac 16+\dfrac{1}{24}+\dfrac 1{5\cdot 4\cdot 3\cdot 2}+\dfrac 1{6\cdot 5\cdot 4\cdot 3}+\cdots +\dfrac{1}{n\cdot (n-1)\cdot (n-2)\cdot (n-3)}+\cdots \\
&=\dfrac{65}{24}+\dfrac 13\left[\dfrac {1}{4\cdot 3\cdot 2}-\dfrac{1}{5\cdot 4\cdot 3}\right]+\dfrac 13\left[\dfrac {1}{5\cdot 4\cdot 3}-\dfrac{1}{6\cdot 5\cdot 4}\right]+\cdots \\
&<\dfrac{65}{24}+\dfrac{1}{72}=\dfrac{49}{18},\end{split} \]而$$\dfrac{49}{18}=1+\dfrac{31}{18}=1+\sqrt{\dfrac{961}{324}}<1+\sqrt 3,$$因此${\rm e}<\sqrt 3+1$．
综上所述，有$\sqrt 7<{\rm e}<\sqrt 3+1<\sqrt 8$．
5．法一 代数方法
即方程$$m\left(x^2+y^2\right)=\left(x-2y+5\right)^2$$表示的曲线是椭圆．令$s=x-2y,t=2x+y$(旋转位似变换)，则方程转化为$$m\left(s^2+t^2\right)=5(s+5)^2,$$即$$(m-5)s^2-50s+mt^2=125.$$该方程表示的曲线为椭圆，则$m>5$．因此$m$的取值范围是$(5,+\infty)$．
法二 数形结合
根据题意，即$$\dfrac{\sqrt{x^2+(y+1)^2}}{\dfrac 1{\sqrt 5}\left|x-2y-3\right|}=\sqrt{\dfrac 5m},$$于是当$m>5$时，方程所表示的曲线是椭圆；当$m=5$时，方程所表示的曲线是抛物线；当$0<m<5$时，方程所表示的曲线是双曲线．
6．如图，作$6\times 9$的矩形$ABCD$，并画两条横线$EF,GH$将矩形长度为$9$的边分为$2,3,4$的三段．在两条横线上分别依次选取$M,N$两点，则$$AM+MN+NC=\sqrt{x^2+4}+\sqrt{y^2+9}+\sqrt{z^2+16}.$$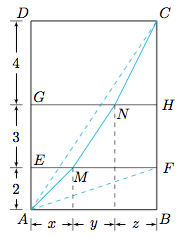
不难证明$$AC\leqslant AM+MN+NC\leqslant AF+FH+HC,$$因此所求的取值范围是$\left[3\sqrt{13},7+2\sqrt{10}\right]$．
下面来证明$AF+FH+HC$最长．先介绍一个引理：
引理 在$\triangle ABC$中，在$\triangle ABC$的内部从$B$到$C$有一条凸的路线$B-D_1-D_2-\cdots-D_n-C$（即多边形$BCD_nD_{n-1}\cdots D_1$是凸多边形），那么有凸多边形的周长小于三角形的周长，也即$$BD_1+D_1D_2+\cdots+D_nC<AB+AC.$$
引理的证明 以$n=2$为例证明，分别延长$BD_1,D_1D_2$交边$AC$于点$E_1,E_2$，如图：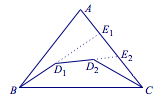
则有$$\begin{cases} AB+AE_1>BD_1+D_1E_1,\\D_1E_1+E_1E_2>D_1D_2+D_2E_2,\\D_2E_2+EC>D_2C,\end{cases}$$左右两边分别相加得$AB+AC>BD_1+D_1D_2+D_2C$．
回到本题 固定$M$点，由引理知，从$MN+NC$的最大值是点$N$在最右边（与点$H$重合）或者最左边（与点$M$在$GH$上的射影重合）时取到，比较这两个值知，点$N$在最右边；同理，当$N$固定时，点$M$在最右边时，$AM+MN$有最大值．所以当$M$在$F$处，$N$在$H$处时有最大值．
7．问题即当$k^2\leqslant 9n+8<(k+1)^2$，$k\in\mathcal N^*$且$k\geqslant 4$时，有$$k\leqslant \sqrt n+\sqrt{n+1}+\sqrt{n+2}<k+1,$$由$k^2\leqslant 9n+8\leqslant (k+1)^2-1$，得$$\dfrac{k^2-8}9\leqslant n\leqslant \dfrac{(k+1)^2-9}9.$$先证明左边不等式．只需要证明$$\sqrt{k^2-8}+\sqrt{k^2+1}+\sqrt{k^2+10}\geqslant 3k,$$即$$3k^2+3+2\sqrt{k^4-7k^2-8}+2\sqrt{k^4+2k^2-80}+2\sqrt{k^4+11k^2+10}\geqslant 9k^2,$$而当$k\geqslant 4$时，有$$\sqrt{k^4-7k^2-8}>k^2-\dfrac 92,\sqrt{k^4+2k^2-80}>k^2-2,\sqrt{k^4+11k^2+10}>k^2+5,$$因此上式$$LHS>3k^2+3+2k^2-9+2k^2-4+2k^2+10=9k^2.$$再证明右边不等式．只需要证明$$\sqrt{(k+1)^2-9}+\sqrt{(k+1)^2}+\sqrt{(k+1)^2+9}<3(k+1),$$即$$\sqrt{(k+1)^2-9}+\sqrt{(k+1)^2+9}<2(k+1),$$根据均值不等式，这是显然的．
综上所述，原命题得证．
思考与总结 正确的将取整符号去掉，并对$n$的范围有一个合理的估计．事实上，相当于证明了$$\sqrt{9n+8}<\sqrt{n}+\sqrt{n+1}+\sqrt{n+2}<\sqrt{9n+9},$$由于$9n+8$与$9n+9$是连续的两个正整数，因此命题成立．