练习题集[34] 基础练习

1、已知函数$f(x)=x+\sin x$，不等式$f(x)\geqslant ax\cos x$在$\left[0,\dfrac{\pi}2\right]$上恒成立，则实数$a$的取值范围是_______．

2、已知实数$a,b$满足$a^3+3a^2+6a=2$，$b^3+3b^2+6b=-10$，则$a+b=$_______．

3、直角坐标平面$xOy$上直线$l$的参数方程为$\begin{cases} x=t\cos\alpha,\\y=t\sin\alpha, \end{cases} $其中$t$为参数，$\alpha\in [0,\pi)$．以原点$O$为极点，$Ox$为极径建立极坐标系，圆$C_1:\rho=2\sin \theta$，圆$C_2:\rho = 2\sqrt 3\cos\theta$，若直线$l$与圆$C_1$交于$A$、$O$，与圆$C_2$交于$B$、$O$，其中$A$、$B$是异于$O$的两点，则线段$AB$长度的最大值为_______．

4、与直线$x+y-2=0$和曲线$x^2+y^2-12x-12y+54=0$都相切的半径最小的圆的标准方程是_______．

5、已知三角形$ABC$的内角$A$、$B$、$C$所对的边分别为$a$、$b$、$c$，$\sin A+\sqrt 2\sin B=2\sin C$，$b=3$，当内角$C$最大时，三角形$ABC$的面积等于_______．

6、如图，互不相同的点$A_1,A_2,\cdots,A_n$和$B_1,B_2,\cdots,B_n$分别在角$O$的两条边上，所有的$A_iB_i$（$i=1,2,\cdots,n$）都相互平行，且所有梯形$A_nB_nB_{n+1}A_{n+1}$的面积均相等，设$OA_n=a_n$，若$a_1=1$，$a_2=2$，则$a_9=$_______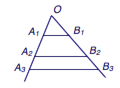． 7、已知$f(x)=x^3+px^2+qx$在$x=x_0$处与$x$轴相切，且$f(x)$的极小值为$-4$，若$x_0\ne 0$，则$p+q=$_______．

参考答案

1、$\left(-\infty ,2\right ]$    

提示    分析端点$x=0$即得．

2、$-2$

提示    问题即$(a+1)^3+3(a+1)=6$，$(b+1)^3+3(b+1)=-6$．注意到$$y=(x+1)^3+3(x+1)$$是单调递增且关于$(-1,0)$对称的函数，于是$$a+1=-(b+1),$$因此$a+b=-2$．

3、$4$

提示    $|AB|=2\sin \alpha-2\sqrt 3\cos \alpha$．

4、$(x-2)^2+(y-2)^2=2$

5、$\dfrac{9+3\sqrt 3}4$

提示    用余弦定理可得当$3a^2=2b^2$时，$C$最大，此时$C$的余弦值为$\dfrac{\sqrt 2}4\left(\sqrt 3-1\right)$．

6、$5$

提示    数列$\{a_n^2\}$是一个等差数列．

7、$15$

提示    根据题意，有$$f(x)=x(x-x_0)^2,$$且$x_0<0$，函数$f(x)$在$(x_0,0)$上取得极小值． 当\(x\in(x_0,0)\)时，由均值不等式有$$f(x)=-\dfrac 12\cdot (-2x) \cdot (x-x_0)\cdot (x-x_0)\geqslant -\dfrac 12\cdot\left(\dfrac{-2x_0}3\right)^3=-4,$$于是可得$$x_0=-3,$$进而由三次方程的韦达定理$$p+q=-2x_0+x_0^2=15.$$