2011年高考江西卷文科数学第10题（选择压轴题）：
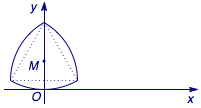
如图，一个“凸轮”放置于直角坐标系\(x\)轴上方，其“底端”落在原点处，一顶点及中心在\(y\)轴正半轴上，它的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．
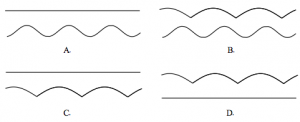
今使“凸轮”沿\(x\)轴正向滚动前进，在滚动过程中，“凸轮”每时每刻都有一个“最高点”，其中心也在不断移动位置，则在“凸轮”滚动一周的过程中，将其“最高点”和“中心点”所形成的图形按上下放置，应大致为（ ）
正确答案是 A．
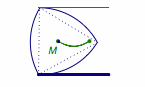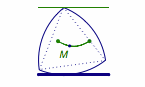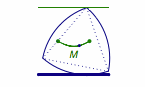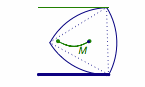
解 凸轮的滚动实际上由交替的滚动（接触点不断变化）和转动（接触点不变）形成．
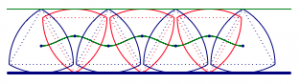
滚动的部分如图．
注意若不考虑其中的平动，只考虑转动（事实上，滚动就是平动与转动的合成），则旋转的中心为与\(x\)轴接触的弧对应的圆心．
转动的部分如图．
注意转动的中心为与\(x\)接触的凸轮内正三角形的顶点．
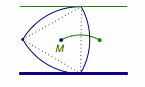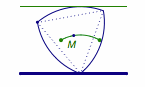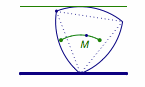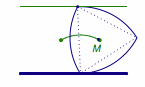
经过分析可知任何时候凸轮的宽度均相等，且其中心离\(x\)轴的距离在正三角形的内切圆半径和外接圆半径之间周期变化，且在初始位置时取得最小值，如图．这样就可得到了正确答案是 A．
既然“凸轮”始终是等宽的，那么能否利用这一性质让它充当自行车的轮子呢？
事实上，这个凸轮就是著名的“勒洛三角形”．勒洛三角形是典型的定宽曲线，在很多领域都能看到它的身影．下图就是柏林一家博物馆内的定宽曲线滚木．另外定宽曲线还有一个有趣的性质，就是宽度相等的定宽曲线有相同的周长，所以下图中的圆形滚木转过一周的时候，旁边的勒洛三角形滚木也恰好转过一周．
勒洛三角形可以用来充当“滚木”
在美国旧金山，有一些市政检修井井盖的形状就是勒洛三角形，其最大优点是这种形状的井盖绝不会掉到井里去．
美国旧金山市政井盖
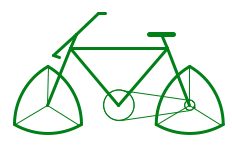
勒洛三角形不能用作轮子，因为其中心并不稳定，每旋转一圈会有三次跳动．不过我国劳动人民就充分发挥聪明才智制造了一辆利用等宽曲线轮的角轮自行车 ，据说已经成功申请专利了．
利用等宽曲线轮的角轮自行车
有人会说“角轮自行车”只是观赏性大于实用性的玩具，确实如此．那不妨让我们再来看看等宽曲线在汽车工业上的应用．当然，汽车制造商们不会用等宽曲线制造轮子，他们把等宽曲线藏在了汽车更核心的部分——发动机里．下图就是马自达公司的转子发动机截面图。其实转子发动机并不是什么新鲜发明，早在 20 世纪 50 年代德国工程师汪克尔就制造出了第一台转子发动机的样机，因此这种发动机又叫做汪克尔发动机．
利用勒洛三角形的转子
许多国家的硬币喜欢采用等宽曲线作为外形轮廓，例如英国的 20 便士与 50 便士银币采用的就是由 7 条弧组成的定宽曲线．除此之外，在不少艺术品中也常常能看到各种等宽曲线的身影，这主要是为了提高观赏价值了．
英国的二十便士硬币
注 后半段有关“勒洛三角形”的介绍转载自果壳网《和圆一样的三角形》．
请问用Mathematica怎么画动图，哪里有教程可以学