函数的零点问题常见的处理思路有两种，一种思路是将一个函数的零点问题转化成两个（较简单的）函数的交点问题，再结合图象进行判断，需要注意的是函数本身可以进行适当的代数变形以使得转化成的两个函数的草图更容易作出；另一种思路是将这个函数作为整体进行考虑，借助这个函数的性质直接得到结果，有时函数的性质需要借助导数去研究．
2014年湖南高考理科第10题（选择压轴题）：
已知函数f(x)=x2+ex−12,x<0与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点，则a的取值范围是_______．
正确答案是(−∞,√e).
解 两个函数图象上存在关于y轴对称的点，即存在点(x,y)与(−x,y)分别在两个函数的图象上．不妨设x>0，有{y=g(x)=x2+ln(x+a),y=f(−x)=x2+e−x−12.
即方程ln(x+a)−e−x+12=0
有正的实数解．
思路一 分治
考虑将方程的解的问题转化成两个函数的交点问题，方程ln(x+a)=e−x−12.
有正根，即函数y=ln(x+a)与y=e−x−12在y轴右侧有交点．如图：
当两个函数图象的交点在A的右侧时，满足情况，所以a<√e.
思路二 归并
记函数h(x)=ln(x+a)−e−x+12，x>0
因为h(x)在定义域(l,+∞)(l=max{−a,0})上是增函数，所以可以直接根据零点存在的条件得到参数范围：
当x→+∞时，h(x)→+∞；只需当x→l时，h(x)可以取到负值即可．于是有(a>0)∧(lna−1+12<0),
或a<0.
解得a<√e.
下面给出一道练习
已知函数g(x)=a−x,1e⩽x⩽e与h(x)=lnx的图象上存在关于x轴对称的点，则实数a的取值范围是____．
答案 [1,e−1].
更多零点问题参见函数零点问题小结，以及每日一题[145]分段函数的零点．
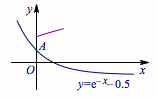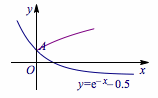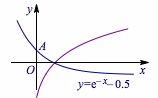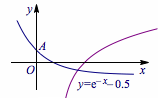
找了一些材料来看，大概理解端点效应的思想了，有时候是需要一定极限知识，否则似乎不方便判断
极限、边界、转折点的想法往往是解决问题的突破口．
思路2的x趋近于L是什么意思，老师能说下嘛？顺便这个解法是端点效应的应用吗？端点效应老师能不能推荐个参考资料链接？谢谢！
本题中，a的正负会影响定义域的左边界，比如当a>0时，h(x)的定义域为(0,+∞)，此时考虑当x越来越接近于0时，函数值趋近于lna−e0+12，这个值小于零即可保证函数存在零点．
每日一题的281,241,157,150,98都是说端点分析的，你可以都找来看看，右边工具栏搜索中搜“端点”即可找到相关文章．