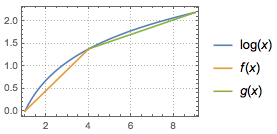
已知函数\(f(x)=\ln x-ax^2\),其中\(a>0\).若存在\(x_1,x_2\in [1,3]\),且\(x_1-x_2\geqslant 1\),使得\(f\left(x_1\right)=f\left(x_2\right)\),求证:\(\dfrac{\ln 3-\ln 2}{5}\leqslant a\leqslant \dfrac{\ln 2}{3}\).
证明 根据已知,有\[\begin{eqnarray}\begin{cases}\ln x_1-ax_1^2=0,\\\ln x_2-ax_2^2=0,\end{cases}\end{eqnarray}\]观察欲证不等式的形式,将 (1) 中的两式相减,可得\[a=\dfrac{\ln x_1-\ln x_2}{x_1^2-x_2^2},\]于是欲证不等式可以变形为\[\begin{eqnarray}\dfrac{\ln 9-\ln 4}{9-4}\leqslant \dfrac{\ln x_1^2-\ln x_2^2}{x_1^2-x_2^2}\leqslant \dfrac{\ln 4-\ln 1}{4-1}.\end{eqnarray}\]
将 (2) 中的代数式用图形表示,可知由\[\begin{eqnarray}1\leqslant x_2^2\leqslant 4\leqslant x_1^2\leqslant 9\end{eqnarray}\]可得欲证不等式成立.
得到了几何图形的支持以后,需要给出严格的证明.
事实上,可以根据几何图形证明一个更强的结论:
引理 当\(x_1^2\)或\(x_2^2\)增大时,\(2a\)的取值\(\dfrac{\ln x_1^2-\ln x_2^2}{x_1^2-x_2^2}\)均减少.
引理的证明 记\(F=\dfrac{\ln u-\ln v}{u-v}\),则\[F_u'=\dfrac{\ln\dfrac{v}{u}+1-\dfrac{v}{u}}{\left(u-v\right)^2},\]而\[\forall \dfrac vu>0\land u\neq v,\ln\dfrac vu<\dfrac vu-1,\]于是\(F_u'< 0\),进而可得当\(x_1^2\)增大时,\(2a\)的取值减小.同理可得当\(x_2^2\)增大时,\(2a\)的取值也减小.
这样一来,对 (3) 应用引理即有结论.
接下来,可以将解法改写.
由于函数\(f(x)\)的导函数为\[f'(x)=\dfrac {1-2ax^2}{x},\]在区间\([1,3]\)上存在两个点\(f(x)\)的函数值相同,于是\(f(x)\)必然存在区间上的极值点,因此函数\(f(x)\)在区间\(\left(1,\dfrac{\sqrt{2a}}{2a}\right)\)上单调递增,在区间\(\left(\dfrac{\sqrt {2a}}{2a},3\right)\)上单调递减.于是\[f(1)\leqslant f(2)\land f(2)\geqslant f(3),\]整理即得欲证不等式.
注 先通过发现题目的几何解释,然后在几何层面上加强结论,再回到代数层面给出简洁的解答是数形结合思想的核心,也是研究函数问题时的重要“修炼”手段.