2012年高考四川卷理科数学第21题(解析几何大题):
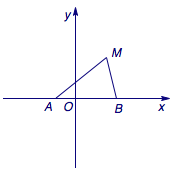
如图,动点\(M\)与两定点\(A(-1,0)\)、\(B(2,0)\)构成三角形\(MAB\),且\(\angle MBA=2\angle MAB\),设动点\(M\)的轨迹为\(C\).
(1)求轨迹\(C\)的方程;
(2)设直线\(y=-2x+m\)与\(y\)轴相交于点\(P\),与轨迹\(C\)相交于点\(Q\)、\(R\),且\(|PQ|<|PR|\),求\(\dfrac{|PR|}{|PQ|}\)的取值范围.
解 注意到倍角条件,可以作角平分线构造等腰三角形转化条件.
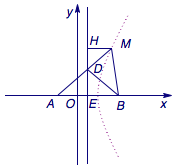
(1)作\(\angle MBA\)的角平分线交\(MA\)于\(D\),过\(D\)作\(x\)轴的垂线,垂足为\(E\),过\(M\)作\(DE\)的垂线,垂足为\(H\),如图.
根据已知条件可得\(\angle DAB=\angle DBA\),于是\(DE\)为线段\(AB\)的垂直平分线,为定直线\(x=\dfrac 12\).由角平分线定理,可得\[\dfrac{BM}{BA}=\dfrac{DM}{DA},\]再由三角形\(DMH\)与三角形\(DAE\)相似可得\[\dfrac{DM}{DA}=\dfrac{MH}{AE},\]于是\[\dfrac{BM}{BA}=\dfrac{MH}{AE},\]从而\[\dfrac{MB}{MH}=\dfrac{BA}{AE}=2\]为定值.
进而由双曲线的第二定义不难得到所求的轨迹方程为\[x^2-\dfrac{y^2}{3}=1,x>1.\]
(2)设\(Q\left(x_1,y_1\right)\),\(R\left(x_2,y_2\right)\),\(\dfrac{x_2}{x_1}=\lambda\),\(\lambda>1\).
联立直线与双曲线方程,可得\[x^2-4mx+m^2+3=0,\]该方程在\((1,+\infty)\)内有两个相异实根,于是可得\(m>1\land m\neq 2\).
根据韦达定理,有\[\left(4m\right)^2=\left(2+\lambda+\dfrac{1}{\lambda}\right)\cdot\left(m^2+3\right),\]化简得\[\lambda+\dfrac{1}{\lambda}=\dfrac{16m^2}{m^2+3}-2,\]于是\(\lambda+\dfrac{1}{\lambda}\)的取值范围是\(\left(2,\dfrac{50}{7}\right)\cup\left(\dfrac{50}{7},14\right)\),进而不难得到\(\lambda\)的取值范围是\(\left(1,7\right)\cup\left(7,7+4\sqrt 3\right)\).
注 (2)中用到了拓展的韦达定理,对于关于\(x\)的一元二次方程\(ax^2+bx+c=0\),若其判别式\(\Delta\geqslant 0\),两根分别为\(x_1\)、\(x_2\),则
两根之和\(x_1+x_2=-\dfrac ba\);
两根之积\(x_1x_2=\dfrac ca\);
两根之差的绝对值\(\left|x_1-x_2\right|=\dfrac{\sqrt \Delta}{|a|}\);
当方程的两根均不为\(0\)时,两根之比\(\lambda\)满足\(b^2=\left(2+\lambda+\dfrac{1}{\lambda}\right)ac\).
下面给出一道练习题:
已知\(b,c\in\mathcal R\),若关于\(x\)的不等式\(0\leqslant x^2+bx+c\leqslant 4\)的解集为\(\left[x_1,x_2\right]\cup\left[x_3,x_4\right]\)(\(x_2<x_3\)),则\(\left(2x_4-x_3\right)-\left(2x_1-x_2\right)\)的最小值是________.
参考答案 \(4\sqrt 3\).