每日一题[242] 图象的伸缩

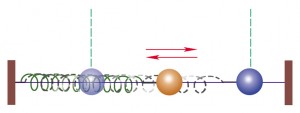
正弦型函数$y=A\sin(\omega x+\varphi)+B$中最富有变化的参数是$\omega$，$\omega$的变化相当于弹簧的压缩（$\omega>1$）或拉伸（$\omega<1$），其中函数图象与$y$的交点为弹簧的固定点，各点到$y$轴的距离成比例变化．

从图象伸缩的角度可以对正弦型函数中的参数$\omega$有更直观的认识，有时可以大大简化计算：

2015年全国高中数学联合竞赛A卷第７题：

设$\omega$为正实数，若存在$a,b$（$\mathrm{\pi}\leqslant a<b\leqslant 2\mathrm{\pi}$），使得$\sin\omega a+\sin\omega b=2$，则$\omega$的取值范围是_______．

正确的答案是$\left[\dfrac 94,\dfrac 52\right]\cup\left[\dfrac{13}{4},+\infty\right)$．

解    由$\sin x\in[-1,1]$知，本题条件可以转化成

存在$a,b\in[\mathrm{\pi},2\mathrm{\pi}]$,$a\ne b$，使得$\sin\omega a=\sin\omega b=1$．

也即$y=\sin \omega x$在$[\mathrm{\pi},2\mathrm{\pi}]$上存在两个不同的最大值点．

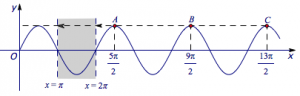
$y=\sin\omega x$的曲线由正弦曲线$y=\sin x$在横方向上进行伸缩得到的，且必有$\omega>1$，即图象一定会进行压缩，如图：

当最大值点$A,B,C,\cdots$中至少存在两个点经过压缩进入阴影区域时，满足题意．

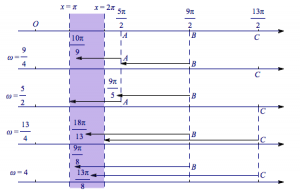
考虑最大值点$A,B,C,\cdots$恰好压缩到边界$\mathrm{\pi}$与$2\mathrm{\pi}$时$\omega$的值，如下：

易知当$\omega$从$1$逐渐增大时，$A$点先到达右边界$2\mathrm{\pi}$，此时不满足条件，当$B$点到达右边界时开始满足，直到$A$点到达左边界$\mathrm{\pi}$，故$\omega\in\left[\dfrac 94,\dfrac 52\right]$时，满足题意；

之后，$\omega$继续增加时，$A$出左边界，只有$B$点在区域内，此时不满足，直到$\omega=\dfrac{13}{4}$时，$C$点压缩到右边界，此时$B,C$两个最值点都在区域内，重新满足条件，直到$B$出左边界，此时需要考虑$C$右边下一个最大值点．

但因为此时$\omega=\dfrac {9}{2}>4$，边界内已经存在至少两个周期，故此时区域内至少含有两个最大值点，一定满足条件，故$\omega\geqslant \dfrac {13}{4}$时一定满足．

最后给一道练习题．

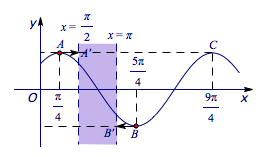
（2012·新课标·理9）已知$\omega>0$，函数$f(x)=\sin\left(\omega x+\dfrac{\mathrm{\pi}}{4}\right)$在$\left(\dfrac{\mathrm{\pi}}{2},\mathrm{\pi}\right)$上单调递减，则$\omega$的取值范围是_____．

答案    $\left[\dfrac 12,\dfrac 54\right]$.

提示    如图．