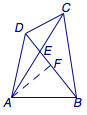
在四边形\(ABCD\)中,\(AB=AD\),\(\angle CAB=3\angle CAD\),\(\angle ACD=\angle CBD\)且为锐角,求\(\tan\angle ACD\).

正确答案为\(\dfrac{\sqrt 3}{3}\).
一个常见的漂亮解法是这样的:
设\(AC\)与\(BC\)交于\(E\),取\(BD\)的中点\(F\),设\(\angle CAD=\alpha\),\(\angle ACD=\beta\),\(AD=AB=1\).
在三角形\(ABD\)中,有\[\begin{eqnarray}BD=2\sin{2\alpha},\end{eqnarray}\]在三角形\(ACD\)中,由正弦定理有\[\begin{eqnarray}CD=\dfrac{\sin\alpha}{\sin\beta},\end{eqnarray}\]在三角形\(BCD\)中,有\[\angle DCB=\angle ECB+\beta=\angle DEC=\dfrac{\pi}2-\alpha,\]从而应用正弦定理\[\dfrac{CD}{\sin\beta}=\dfrac{BD}{\sin\left(\dfrac{\pi}{2}-\alpha\right)},\]将(1)(2)代入,即得\[\sin\beta=\dfrac 12,\]于是所求值为\(\dfrac{\sqrt 3}3\).
这里得到(1)(2)后分析三角形\(BCD\)颇有技巧,那么如果没有注意到其中的角度关系,该如何解决这个问题呢?
我们知道,解几何题时可以通过重新作图理顺几何条件,并从中梳理出核心条件,那么对于此题,可以尝试作图.
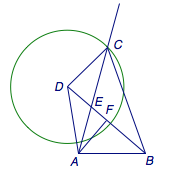
1、作一个等腰三角形\(BAD\),其中\(AB=AD\);
2、取\(BD\)中点\(F\),连接\(AF\),作\(\angle DAF\)的平分线,设角平分线与\(BD\)交于\(E\);
3、注意到\(\angle ACD=\angle CBD\),这是典型的“反平行”相似模型,于是三角形\(CDE\)和三角形\(BDC\)相似,于是\(CD^2=DE\cdot DB\).因此以\(D\)为圆心\(\sqrt{DE\cdot DB}\)为半径作圆,与\(\angle DAF\)的平分线交于\(C\)点;
4、最后连接\(CD\)、\(CB\)就完成了作图.
根据作图步骤,\(DB=2\sin2\alpha\),\(DE=\sin {2\alpha}-\cos{2\alpha}\cdot\tan \alpha\),于是在三角形\(ACD\)中应用正弦定理,有\[\sin\beta=\dfrac{\sin\alpha}{\sqrt{DB\cdot DE}},\]进而代入\(DB\)、\(DE\)的值可以计算得\(\sin\beta=\dfrac 12\).
注 通过作图的方式,我们还得到了在该题中\(\angle CAD\)是可以变化的角,而\(\angle ACD\)不会受其影响,恒为\(\dfrac{\pi}6\).