2014年高考江西卷文科数学第15题(填空压轴题):
\(x,y\in\mathcal R\),若\(|x|+|y|+|1-x|+|1-y|\leqslant 2\),则\(x+y\)的取值范围是_______.
解 我们熟知\[|x|+|1-x|\geqslant |x+(1-x)|=1,\]等号当且仅当\(0\leqslant x\leqslant 1\)时取得,类似的,亦有\[|y|+|1-y|\geqslant |y+(1-y)|=1,\]等号当且仅当\(0\leqslant y\leqslant 1\)时取得,于是题意即\[\begin{cases}0\leqslant x\leqslant 1,\\0\leqslant y\leqslant 1,\end{cases}\]该不等式组表示的可行域如图所示,于是\(x+y\)的取值范围是\([0,2]\).
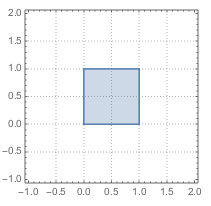
接下来思考一个扩展的问题,如果不等式右边的\(2\)改成\(3\),可行域将会发生什么样的改变?
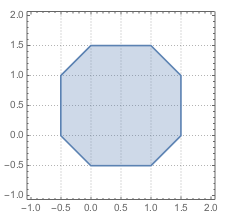
如图,将按\(x\)方向上的两个分点\(x=0\)和\(x=1\),\(y\)方向上的两个分点\(y=0\)和\(y=1\)将平面区域划分为\(9\)个部分,在每个部分分别研究图象可得可行域将变成一个八边形,每条边的斜率均为\(\pm 1\)或\(0\),所求\(x+y\)的范围变为\(\left[-\dfrac 12,\dfrac 52\right]\).
那么更一般的,如果可行域变为\(m\),其中\(m>2\),所求\(x+y\)的范围会发生什么样的变化呢?
如图,可行域仍然会保持八边形的形状,所求\(x+y\)的取值范围为\(\left[1-\dfrac m2,1+\dfrac m2\right]\).
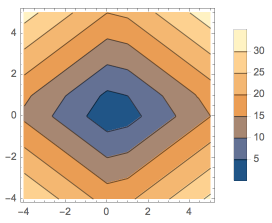
注 \(|2x|+|3y|+|1-x|+|2-y|\)的等高线如图.



Pingback引用通告: 目标函数比值型的规划问题 | Math173
Pingback引用通告: 每周一招[10]目标函数比值型的规划问题(高一) | 数海拾贝内容系统
等号当且仅当−1⩽x⩽1时取得,这里打错了吧。应该是等号当且仅当0⩽x⩽1时取得
另外,老师能不能开个帖子讲解一下\[f\left( x \right) = \sum\limits_{i=1}^n {\left( {{a_i} \cdot \left| {x - {b_i}} \right|} \right)} \]的相关特性啊……
嗯,已修正.