2014年全国高中数学联赛河南省预赛第6题：
\(65^{1000}-8^{2001}\)的值与零的大小关系为_______．
正确答案是大于．
只需要比较\((64+1)^{1000}\)与\(8\cdot 64^{1000}\)的大小关系，也即比较\(\left(1+\dfrac{1}{64}\right)^{1000}\)与\(8\)的大小关系．
事实上，我们有\[\left(1+\dfrac{1}{64}\right)^{1000}>1+\dfrac{1}{64}\cdot 1000>8,\]于是正确的答案是大于．
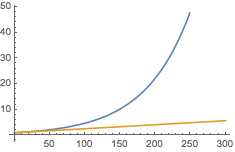
注 推理过程中用到了伯努利不等式．图中的曲线和直线分别为\(y=\left(1+\dfrac{1}{64}\right)^x\)与\(y=1+\dfrac{x}{64}\)的图象，可以看到随着\(x\)的增大，后来两者的差距明显拉开．