每日一题[194] 向量分解的系数和

2014年全国高中数学联赛河北省预赛第7题：

已知圆$O:x^2+y^2=1$为三角形$ABC$的外接圆，且$\tan A=2$，若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$，则$x+y$的最大值为_______．

---

正确答案是$\dfrac{5-\sqrt 5}{4}$．

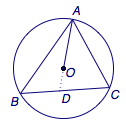
如图，延长$AO$交边$BC$于点$D$，设$\overrightarrow{AO}=\lambda \overrightarrow{AD}$，则有

$$\overrightarrow{AD}=\dfrac {x}{\lambda}\overrightarrow{AB}+\dfrac{y}{\lambda}\overrightarrow{AC},$$ 于是由平面向量共线的表达可得 $$\dfrac{x}{\lambda}+\dfrac{y}{\lambda}=1,$$ 从而可得 $$x+y=\lambda=\dfrac{AO}{AD},$$ 显然，当$OD$取最小值时$x+y$取得最大值，此时三角形$ABC$为等腰三角形，容易计算得$x+y=\dfrac{5-\sqrt 5}{4}$．