2015年高考重庆卷理科数学第10题(选择压轴题):
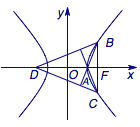
设双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)(\(a,b>0\))的右焦点为\(F\),右顶点为\(A\),过\(F\)作\(AF\)的垂线与双曲线交于\(B\)、\(C\)两点,过\(B\)、\(C\)分别作\(AC\)、\(AB\)的垂线,两垂线交于点\(D\).若\(D\)到直线\(BC\)的距离小于\(a+\sqrt{a^2+b^2}\),则该双曲线的渐近线斜率的取值范围是( )
A.\(\left(-1,0\right)\cup\left(0,1\right)\)
B.\(\left(-\infty,-1\right)\cup\left(1,+\infty\right)\)
C.\(\left(-\sqrt 2,0\right)\cup\left(0,\sqrt 2\right)\)
D.\(\left(-\infty,-\sqrt 2\right)\cup\left(\sqrt 2,+\infty\right)\)
如图,根据已知条件\(\triangle BDF\)与\(\triangle ABF\)相似,于是\[BF^2=AF\cdot DF,\]即\[DF=\left(\dfrac{b^2}{a}\right)^2\cdot\dfrac{1}{c-a}<a+\sqrt{a^2+b^2}=c+a,\]整理得\[b^2<a^2,\]于是该双曲线渐近线的斜率的取值范围是\(\left(-1,0\right)\cup\left(0,1\right)\),