每日一题[162]参数方程与仿射变换

2015年高考湖北卷理科数学第21题（解析几何大题）：

一种作图工具如图所示．\(O\)是滑槽\(AB\)的中点，短杆\(ON\)可绕\(O\)转动，长杆\(MN\)通过\(N\)处铰链与\(ON\)连接，\(MN\)上的栓子可沿滑槽\(AB\)滑动，且\(DN=ON=1\)，\(MN=3\)．当栓子\(D\)在滑槽\(AB\)内作往复运动时，带动\(N\)绕\(O\)转动一周（\(D\)不动时，\(N\)也不动），\(M\)处的笔尖画出的曲线记为\(C\)．以\(O\)为原点，\(AB\)所在的直线为\(x\)轴建立平面直角坐标系．

（1）求曲线\(C\)的方程；

（2）设动直线\(l\)与两定直线：\(l_1:x-2y=0\)和\(l_2:x+2y=0\)分别交于\(P\)、\(Q\)两点．若直线\(l\)总与曲线\(C\)有且只有一个公共点，试探究：\(\triangle OPQ\)的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．

（1）解    设\(N\left(\cos\theta,\sin\theta\right)\)，则\(D\left(2\cos\theta,0\right)\)，于是由\[\overrightarrow{NM}=-\dfrac 32\overrightarrow{MD}\]得\[M\left(\dfrac{x_N-\frac 32x_D}{1-\frac 32},\frac{y_N-\frac 32y_D}{1-\frac 32}\right)=M\left(4\cos\theta,-2\sin\theta\right),\]于是可得曲线\(C\)的方程为\[\frac{x^2}{16}+\frac{y^2}{4}=1.\]

（2）解    存在最小值，最小值为\(8\)．证明如下：

在伸缩变换\[\begin{pmatrix}x'\\y'\end{pmatrix}=\begin{pmatrix}1&0\\0&2\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}\]下，椭圆\(C\)变为圆\(x'^2+y'^2=16\)．而在变换后直线\(l_1'\)和\(l_2'\)则变为互相垂直的直线\(x'-y'=0\)和\(x'+y'=0\)，如图．

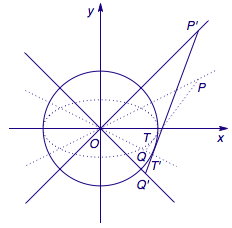记切点\(T\)变换后的点为\(T'\)，则\(P'Q'\)与圆相切于\(T'\)，从而\[\begin{split}S_{\triangle OP'Q'}&=\frac 12OT'\cdot P'Q'\\&=2\left(P'T'+Q'T'\right)\\&\geqslant 4\sqrt{P'T'\cdot Q'T'}\\&=16,\end{split}\]等号当\(P'T'=Q'T'\)时取得．因此\(\triangle OPQ\)的面积\[S_{\triangle OPQ}=\frac 12S_{\triangle OP'Q'}\geqslant 8,\]于是其最小值存在，且为\(8\)．

注    本题所用的参数方程以及仿射变换方法可以参见2011年高考数学山东卷压轴题的两种解法．