2015年高考数学天津卷理科第20题（压轴题）：
已知函数\(f(x)=nx-x^n\)，\(x\in\mathcal R\)，其中\(n\in\mathcal N^*\)，且\(n\geqslant 2\)．
（1）讨论\(f(x)\)的单调性；
（2）设曲线\(y=f(x)\)与\(x\)轴正半轴的交点为\(P\)，曲线在点\(P\)处的切线方程为\(y=g(x)\)，求证：对于任意的正实数\(x\)，都有\(f(x)\leqslant g(x)\)；
（3）若关于\(x\)的方程\(f(x)=a\)（\(a\)为实数）有两个正实数根\(x_1\)、\(x_2\)，求证：\(\left|x_1-x_2\right|<\dfrac{a}{1-n}+2\)．
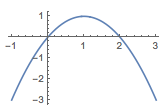
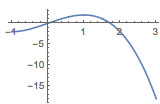
（1）解 根据题意，有\[f'(x)=n-nx^{n-1},\]于是当\(n\)为奇数时，函数\(f(x)\)在\((-\infty,-1)\)上单调递减，在\((-1,1)\)上单调递增，在\((1,+\infty)\)上单调递减；当\(n\)为偶数时，函数\(f(x)\)在\((-\infty,1)\)上单调递增，在\((1,+\infty)\)上单调递减，如图．
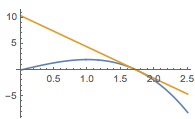
（2）证明 根据题意，\(P\)的坐标为\(P\left(n^{\frac 1{n-1}},0\right)\)，于是曲线在点\(P\)处的切线方程为\[g(x)=\left(n-n^2\right)\left(x-n^{\frac{1}{n-1}}\right),\]进而\[g(x)-f(x)=x^n-n^2x+(n^2-n)\cdot n^{\frac{1}{n-1}},\]其导函数为\[\left(g(x)-f(x)\right)'=nx^{n-1}-n^2,\]于是函数\(g(x)-f(x)\)在\(x=n^{\frac{1}{n-1}}\)处取得极小值，同时也为最小值\(0\)．因此原命题得证，如图．
（3）证明 显然符合题意的\(a>0\)．不妨设\(0<x_1<x_2<n^{\frac{1}{n-1}}\)，以下所有函数的定义域均默认为\(\left[0,n^{\frac 1{n-1}}\right]\)．
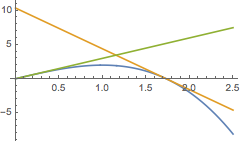
考虑函数\(f(x)\)在\(x=0\)处的切线\[h(x)=nx,\]由于\[h(x)-f(x)=x^n\geqslant 0,\]于是可得\[f(x)\leqslant h(x),\]如图．
因此我们可以利用这两条曲线对\(x_1,x_2\)进行线性估计（以直代曲）．设\[f\left(x_1\right)=h\left(x_3\right)=g\left(x_4\right)=f\left(x_2\right)=a,\]则有\[x_3<x_1<x_2<x_4,\]于是有\[\begin{split}\left|x_1-x_2\right|&<x_4-x_3\\&=\left(\dfrac{a}{n-n^2}+n^{\frac{1}{n-1}}\right)-\dfrac{a}{n}\\&=\dfrac{a}{1-n}+n^{\frac{1}{n-1}},\end{split}\]接下来只需要证明\[n^{\frac{1}{n-1}}\leqslant 2,\]即\[n\leqslant 2^{n-1}.\]事实上，根据二项式定理，有\[2^{n-1}=(1+1)^{n-1}\geqslant 1+{\rm C}_{n-1}^1=n,\]等号当且仅当\(n=2\)时取得．因此原命题得证．
注 利用函数在某一点处的切线得到函数的线性上界（或下界）是处理和函数相关的不等式的重要方法．事实上，常用的不等式有很多都是这样得来的，如\[\sin x\leqslant x,{\rm e}^x\geqslant x+1,\ln(x+1)\leqslant x,\cdots\]以上各式中\(x\)均在区间\([0,+\infty)\)．