每日一题[143] 分离参数

2015年新课标I卷高考数学理科试题第12题（选择最后一题）：

设函数$f(x)={\rm e}^x(2x-1)-ax+a$，其中$a<1$，若存在唯一的整数$x_0$，使得$f(x_0)<0$，则$a$的取值范围是（        ）

A．$\left[-\dfrac{3}{2{\rm e}},1\right)$

B．$\left[-\dfrac{3}{2{\rm e}},\dfrac 34\right)$

C．$\left[\dfrac{3}{2{\rm e}},\dfrac 34\right)$

D．$\left[\dfrac{3}{2{\rm e}},1\right)$

---

正确答案是D．

考虑函数$g(x)={\rm e}^x(2x-1)$，以及函数$h(x)=a(x-1)$，则题意要求存在唯一的整数$x_0$使得$g(x_0)<h(x_0)$．

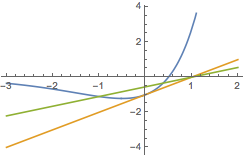
注意到

$$g'(x)={\rm e}^x(2x+1),$$ 尤其注意到$y=x-1$为$y=g(x)$在$(0,-1)$处的切线，如图．

于是可以确定符合题意的唯一整数$x_0=0$，进而可得$a$的取值范围．