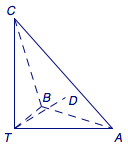
在三棱锥\(T-ABC\)中，\(TA,TB,TC\)两两垂直，\(T\)在平面\(ABC\)上的投影为\(D\)，\(O\)为三棱锥\(T-ABC\)内任意一点，连接\(AO\)、\(BO\)、\(CO\)、\(TO\)并延长交对面于\(A'\)、\(B'\)、\(C'\)、\(T'\)，给出下列命题：
① \(TA\perp BC\)，\(TB\perp AC\)，\(TC\perp AB\)；
② \(\triangle ABC\)是锐角三角形；
③ \(\dfrac{1}{TD^2}=\dfrac{1}{TA^2}+\dfrac{1}{TB^2}+\dfrac{1}{TC^2}\)；
④ \(S_{\triangle ABC}^2=\dfrac 13\left(S_{\triangle TAB}^2+S_{\triangle TAC}^2+S_{\triangle TBC}^2\right)\)（注：\(S_{\triangle ABC}\)表示三角形\(ABC\)的面积）；
⑤ \(\dfrac{OA'}{AA'}+\dfrac{OB'}{BB'}+\dfrac{OC'}{CC'}+\dfrac{OT'}{TT'}=1\)．
其中正确的是_______．（写出所有正确命题的编号）
正确答案是①②③⑤．
① 根据题意有\(TA\perp TBC\)，于是\(TA\perp BC\)．同理，\(TB\perp CA\)，\(TC \perp AB\)，命题正确；
② 设\(TA=a\)，\(TB=b\)，\(TC=c\)，则\[\begin{split}\cos{A}&=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}\\&=\dfrac{\left(a^2+b^2\right)+\left(a^2+c^2\right)-\left(b^2+c^2\right)}{2\sqrt{a^2+b^2}\cdot\sqrt{a^2+c^2}}\\&=\dfrac{a^2}{\sqrt{a^2+b^2}\cdot\sqrt{a^2+c^2}}\\&>0,\end{split}\]于是角\(A\)为锐角．同理，角\(B\)、角\(C\)也为锐角，命题正确；
③ 设三角形\(ABC\)的面积为\(S\)，三棱锥\(T-ABC\)的体积为\(V\)．由②得\[\sin A=\dfrac{\sqrt{a^2b^2+b^2c^2+c^2a^2}}{\sqrt{a^2+b^2}\cdot\sqrt{a^2+c^2}},\]于是\[\begin{split}S&=\dfrac 12\cdot AB\cdot AC\cdot\sin A\\&=\dfrac 12\sqrt{a^2b^2+b^2c^2+c^2a^2},\end{split}\]而\[V=\dfrac 13\cdot TC\cdot S_{\triangle TAB}=\dfrac 16abc,\]于是\[TD=\dfrac{V}{\dfrac 13S}=\dfrac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}},\]从而\[\dfrac{1}{TD^2}=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2},\]因此命题正确；
④ 根据③，有\[\begin{split}S^2&=\dfrac 14\left(a^2b^2+b^2c^2+c^2a^2\right)\\&=S_{\triangle TAB}^2+S_{\triangle TBC}^2+S_{\triangle TCA}^2,\end{split}\]因此命题错误．
⑤ 根据空间向量的共面性质，有平面\(ABC\)上的点\(P\)满足\[\overrightarrow{TP}=\lambda\overrightarrow{TA}+\mu\overrightarrow{TB}+\nu\overrightarrow{TC},\]其中\(\lambda+\mu+\nu=1\)．于是若直线\(TP\)上一点\(Q\)满足\(\overrightarrow{TQ}=x\overrightarrow{TP}\)，那么\[\overrightarrow{TQ}=\lambda'\overrightarrow{TA}+\mu'\overrightarrow{TB}+\nu'\overrightarrow{TC},\]其中\(\lambda'+\mu'+\nu'=x\)．
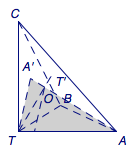在本命题中，令\(P=T'\)，\(Q=O\)，则\[x=1-\dfrac{OT'}{TT'}.\]而另一方面，有\[\dfrac{OA'}{AA'}=\lambda',\dfrac{OB'}{BB'}=\mu',\dfrac{OC'}{CC'}=\nu',\]如图．因此命题正确．