如图,直线 $y=kx-8k$ 交 $x$ 轴于点 $A$,交 $y$ 轴正半轴于点 $B$,且 $\triangle AOB$ 的面积等于 $32$.

1、求直线 $AB$ 的解析式.
2、点 $P$ 为 $OA$ 上一点,连接 $PB$,把线段 $PB$ 绕点 $B$ 顺时针旋转 $90^\circ$ 得到线段 $CB$,连接 $PC$,设点 $P$ 的横坐标为 $m$,四边形 $PABC$ 的面积为 $S$,求 $S$ 与 $m$ 的函数关系式.
3、在第 $(2)$ 小题的条件下,延长 $BC$ 交 $x$ 轴于点 $E$,点 $D$ 在 $EB$ 的延长线上,且 $∠ADB=4\angle CPE$,若 $AD+BD=BE$,求点 $D$ 的坐标.
解析
1、根据题意,有 $A(8,0)$,$B(0,-8k)$,其中 $k<0$,于是 $\triangle AOB$ 的面积\[[AOB]=\dfrac 12\cdot 8\cdot (-8k)=-32k,\]因此 $k=-1$,所求解析式为 $y=-x+8$.
2、根据题意,有\[\begin{split} S&=[PABC]\\ &=[BPA]+[BCP]\\ &=\dfrac 12\cdot AP\cdot OB+\dfrac 12\cdot BP^2\\ &=\dfrac 12\cdot (8-m)\cdot 8+\dfrac 12\cdot (8^2+m^2)\\ &=\dfrac 12m^2-4m+64,\end{split}\]其中 $m$ 的取值范围是 $[0,8]$.
3、延长 $ED$ 至 $F$,使得 $DF=DA$,则根据题意,有\[AD+BD=BE\implies DF+BD=BE\implies BE=BF,\]于是 $F$ 为a $E$ 点关于 $BP$ 的对称点,且 $\angle ADB=2\angle AFB$,从而 $\angle AFB=2\angle CPE$.设 $\angle CPE=x$,则 $\angle BPA=135^\circ-x$,进而 $\angle PBA=x$,于是 $\angle FBA=90^\circ-x$,结合 $\angle AFB=\dfrac 12\angle ADB=2x$,可得 $\angle BAF=90^\circ-x$,因此 $FB=FA$.
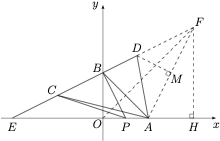
作 $FH\perp EA$ 于 $H$,则 $OB$ 为 $\triangle EHF$ 的中位线,从而 $FH=16$.又 $OA=OB$ 且 $FA=FB$,于是 $OF$ 垂直平分 $AB$,因此 $F$ 在直线 $y=x$ 上,从而 $F(16,16)$.进而直线 $EF$ 的解析式为 $y=\dfrac 12x+8$,设 $D(2t,t+8)$,而 $AF$ 的中点 $M(12,8)$,因此由 $DM\perp AF$ 可得\[\dfrac {(t+8)-8}{2t-12}=-\dfrac 12\iff t=3,\]从而 $D(6,11)$.
事实上,此时 $P(4,0)$,恰为 $OA$ 中点.另外若条件改为 $\angle PDB=4\angle CPE$,则用类似的方法可得 $\angle FEP=2\angle FPE$,于是可得 $\angle CPE=15^\circ$,进而可得 $D\left(8,\dfrac{24+8\sqrt 3}3\right)$.
