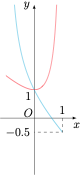已知 $f(x)=x^3+ax^2-x+1-a$,且对任意 $x\in [-1,1]$,$|f(x)|\geqslant |x|$ 恒成立,求实数 $a$ 的取值范围.
答案 $\left(-\infty,-\dfrac 12\right]$.
解析 注意到当 $x=0,\pm 1$ 时,$|f(x)|\geqslant |x|$ 均成立,因此只需要考虑 $x\ne 0,\pm 1$ 的情形.此时不等式 $|f(x)|\geqslant |x|$,即\[ \begin{cases} \forall x\in (0,1),x^3-x+1+a(x^2-1)\geqslant x \lor x^3-x+1+a(x^2-1)\leqslant -x,\\ \forall x\in (-1,0),x^3-x+1+a(x^2-1)\geqslant -x \lor x^3-x+1+a(x^2-1)\leqslant x,\end{cases}\]即\[\begin{cases} \forall x\in (0,1),a\leqslant \dfrac{x^3-2x+1}{1-x^2}\lor a\geqslant \dfrac{x^3+1}{1-x^2},\\ \forall x\in (-1,0),a\leqslant \dfrac{x^3+1}{1-x^2}\lor a\geqslant \dfrac{x^3-2x+1}{1-x^2},\end{cases}\]也即\[\begin{cases} \forall x\in (0,1),a\leqslant -x+\dfrac1{x+1}\lor a\geqslant -x-\dfrac 1{x-1},\\ \forall x\in (-1,0),a\geqslant -x+\dfrac1{x+1}\lor a\leqslant -x-\dfrac 1{x-1},\end{cases}\]画出函数 $g(x)=-x+\dfrac1{x+1}$ 和 $h(x)=-x-\dfrac 1{x-1}$ 的图象可得\[\begin{cases} a\leqslant -\dfrac 12,\\ a\leqslant 1,\end{cases}\iff a\leqslant -\dfrac 12,\]因此所求实数 $a$ 的取值范围是 $\left(-\infty,-\dfrac 12\right]$.