已知 $F_{1}, F_{2}$ 分别是双曲线 $C: \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$($a>0$,$ b>0$)的左、右焦点,过点 $F_{1}$ 向一条渐进线作垂线,交双曲线右支于点 $P$,直线 $F_{2} P$ 与 $y$ 轴交于点 $Q$($P, Q$ 在 $x$ 轴同侧),连接 $Q F_{1}$,若 $\triangle P Q F_{1}$ 的内切圆圆心恰好落在以 $F_{1} F_{2}$ 为直径的圆上,则 $\angle F_{1} P F_{2}$ 的大小为[[nn]];双曲线的离心率 $e$ 为_______.
答案 $90^\circ$;$\sqrt 5$.
解析 如图.
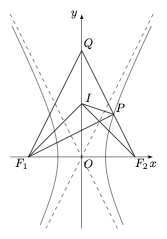
根据题意,$QO$ 平分 $\angle F_1QF_2$,于是 $\triangle QF_1P$ 的内切圆圆心为 $\angle QPF_1$ 的平分线与 $y$ 轴的交点 $I$,且 $\angle QF_1I=\angle PF_1I$.又根据对称性可得 $\angle QF_1I=\angle QF_2I$,于是 $\angle IF_1P=\angle IF_2P$,从而 $F_1,I,P,F_2$ 四点共圆,$\angle F_1PF_2$ 为直角.进而由 $PF_1$ 与渐近线垂直可得 $PF_2:PF_1:F_1F_2=a:b:c$(其中 $c$ 为双曲线的半焦距),从而\[PF_1-PF_2=2a\implies 2b-2a=2a\implies b=2a\implies e=\sqrt 5.\]
