这是2013年北京市春季普通高中会考试题:
已知函数\(f(x)=ax^2+bx+c\)满足:
① \(f(x)\)的一个零点为\(2\);
② \(f(x)\)的最大值为\(1\);
③ 对任意实数\(x\)都有\(f(x+1)=f(1-x)\).
(1)求\(f(x)\)的解析式;
(2)设函数\(g(x)=\begin{cases}x,&x\in A,\\f(x),&x\in B\end{cases}\)是定义域为\((0,1)\)的单调递增函数,\(0<x_0<x'<1\).当\(x_0\in B\)时,证明:\(x'\in B\).
问题的关键在于第2小问.
法一
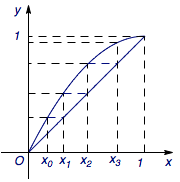
如图,设\(x_n=f\left(x_{n-1}\right)\),其中\(n=1,2,\cdots\).于是由\(x_0\in B\),\(g(x)\)单调递增可知区间\(\left[x_0,x_1\right]\)一定包含于\(B\).(若不然,设\(t\in\left[x_0,x_1\right]\)且\(t\in A\),则\[g(t)=t<x_1=f\left(x_0\right)=g\left(x_0\right),\]矛盾.)
同理可得区间\[\left[x_1,x_2\right],\cdots,\left[x_{n-1},x_n\right],\cdots\]均包含于\(B\).因此只需要证明存在某个\(x_i(i\in\mathcal N^*)\)比\(x'\)大即可.事实上,由\[x_n=f\left(x_{n-1}\right)=2x_{n-1}-x_{n-1}^2,\]可得\[\begin{split}1-x_n&=\left(1-x_{n-1}\right)^2\\&\leqslant \left(1-x_0\right)\cdot\left(1-x_{n-1}\right)\\&\leqslant\left(1-x_0\right)^2\cdot\left(1-x_{n-2}\right)\\&\leqslant \cdots\\&\leqslant \left(1-x_0\right)^n,\end{split}\]考虑到\(0<1-x_0<1\),因此当\(N=\left[{\log_{1-x_0}}{\left(1-x'\right)}\right]+1\)时,必然有\[1-x_N\leqslant\left(1-x_0\right)^N<1-x',\]从而有\[x_N>x',\]因此命题得证.
法二
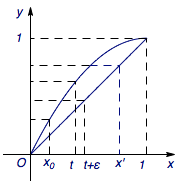
用反证法,设\(x'\in A\),那么对任意\(0<\delta<x'-x_0\),在区间\(\left[x_0,x'\right]\)上必然存在某个长度小于\(\delta\)的子区间\(\left[t,t+\varepsilon\right]\)满足\(t\in B\)且\(t+\varepsilon\in A\).(只要需要将区间\(\left[x_0,x'\right]\)平均分为\(N\)份,其中\(N=\left[\dfrac{x'-x_0}{\delta}\right]+1\),然后逐一考察每个子区间即可.)
于是考虑\[\begin{split}g\left(t+\varepsilon\right)-g(t)&=t+\varepsilon-\left(2t-t^2\right)\\&=\left(t^2-t\right)+\varepsilon\\&\leqslant \max\left\{x_0^2-x_0,x'^2-x'\right\}+\varepsilon,\end{split}\]此时只需要取\[\delta=-\dfrac 12\max\left\{x_0^2-x_0,x'^2-x'\right\}\]就可以使得\[g\left(t+\varepsilon\right)-g(t)<0,\]与\(g(x)\)在\([0,1]\)上单调递增矛盾.
因此\(x'\in B\),原命题得证.