证明:
1、$\dfrac 1{2^k} + \dfrac 1{2^k+1} + \dfrac 1{2^k+2} + \dots +\dfrac 1{2^{k+1}-1} <1$($k \geqslant 2$,$k \in \mathbb N^{\ast}$).
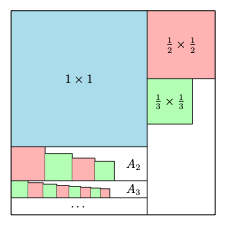
2、分别以 $1,\dfrac 12,\dfrac 13,\cdots,\dfrac 1n,\cdots$ 为边长的正方形能互不重叠地全部放入一个边长为 $\dfrac 32$ 的正方形内.
解析
1、根据题意,有\[LHS=\sum_{i=0}^{2^k-1}\dfrac{1}{2^k+i}<\sum_{i=0}^{2^k-1}\dfrac{1}{2^k}=1,\]命题得证.
2、根据第 $(1)$ 小题的结果,边长为 $\dfrac{1}{2^k+i}$($i=0,1,\cdots,2^k-1$)的共 $2^k$ 个正方形可以互不重叠的并排放在 $1\times \dfrac{1}{2^k}$ 的矩形内.依次取 $k=2,3,\cdots$,边长为 $\dfrac 14,\dfrac 15,\cdots,$ 的正方形可以互不重叠的并排放在\[1\times \dfrac{1}{2^2},1\times \dfrac{1}{2^3},\cdots\]的矩形内.把这些矩形并排放置,而\[\dfrac 1{2^2}+\dfrac1{2^3}+\cdots<\dfrac 12,\]可知这些矩形可以放入 $1\times\dfrac 12$ 的矩形中.综上所述,可以如图放置,其中区域 $A_k$ 放置 $\dfrac{1}{2^k+i}$($i=0,2,\cdots,2^k-1$)共 $2^k$ 个正方形.