每日一题[1285]暴力计算

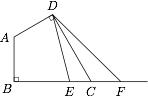
如图，在平面四边形 $ABCD$ 中，$AB\perp BC$，$AD\perp DC$，$AB=AD=1$，$\angle BAD=\dfrac{2\pi}3$，射线 $BC$ 上的两个动点 $E,F$（$E$ 在线段 $BC$ 上，且不与 $B,C$ 重合）满足 $DC$ 平分 $\angle EDF$，则当 $4BE+BF$ 最小时，$\tan\angle EDF$ 的值是_______．

答案    $\sqrt 3$．

解析    如图．连接 $BD$，则 $\triangle BDC$ 为正三角形，建立平面直角坐标系 $B-FA$，则 $D\left(\dfrac{\sqrt 3}2,\dfrac 32\right)$．

设 $\angle EDF=2\theta$，其中 $\theta\in\left(0,\dfrac{\pi}3\right)$，则直线 $DE,DF$ 的倾斜角分别为 $\dfrac{2\pi}3-\theta,\dfrac{2\pi}3+\theta$，设 $BE=m$，$BF=n$，则 $$\dfrac{\dfrac 32}{\dfrac {\sqrt 3}2-m}=\tan\left(\dfrac{2\pi}3-\theta\right),$$ 解得 $$m=\dfrac{3-\sqrt 3\cdot t}{\sqrt 3+t},$$ 其中 $t=\tan\theta$，类似可得 $$n=\dfrac{3+\sqrt 3\cdot t}{\sqrt 3-t},$$ 因此 $$\begin{split} 4BE+BF&=4\cdot \dfrac{3-\sqrt 3\cdot t}{\sqrt 3+t}+\dfrac{3+\sqrt 3\cdot t}{\sqrt 3-t}\\ &=\dfrac{5\sqrt 3\cdot t^2-18t+15\sqrt 3}{3-t^2}\\ &=\dfrac{18}{\dfrac{10}{\sqrt 3}-\left(\dfrac{5}{\sqrt 3}-t+\dfrac{\dfrac{16}3}{\dfrac{5}{\sqrt 3}-t}\right)}-5\sqrt 3\\ &\geqslant 4\sqrt 3,\end{split}$$ 等号当且仅当 $t=\dfrac{1}{\sqrt 3}$，也即 $\theta=\dfrac{\pi}6$ 时取得，此时 $\tan\angle EDF=\sqrt 3$．