每日一题[114]极值点偏移不等式的几种常见处理方法

已知函数$f(x)=a-\dfrac{1}{x}-\ln x$，其中$a\in\mathcal R$．

（1）若$a=2$，求$f(x)$在$\left(1,{\mathrm e}^2\right)$上零点的个数；

（2）若$f(x)$恰有一个零点，求$a$的取值集合；

（3）若$f(x)$有两个零点$x_1,x_2$，且$x_1<x_2$，求证：$2<x_1+x_2<3{\mathrm e}^{a-1}-1$．

---

记函数$g(x)=\dfrac 1x + \ln x$，则

$$g'(x)=\dfrac{x-1}{x^2},$$ 于是可得函数$g(x)$的图象如图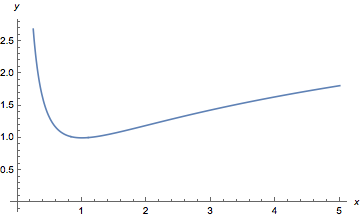． 于是当$a=2$时，$f(x)$在$\left(1,{\mathrm e}^2\right)$上有一个零点； 若$f(x)$恰有一个零点，$a$的取值集合为$\{1\}$； 问题的关键是第三问的不等式的证明．

先证明左边的不等式．

齐次化

根据题意，有

$$\begin{split}\dfrac{1}{x_1}+\ln x_1=a,\\\dfrac{1}{x_2}+\ln x_2=a,\end{split}$$ 两式相减，化简得 $$x_1x_2=\dfrac{x_2-x_1}{\ln{\dfrac{x_2}{x_1}}},$$ 于是可得 $$\begin{split}x_1=\dfrac{1-\dfrac{x_1}{x_2}}{\ln{\dfrac{x_2}{x_1}}},\\x_2=\dfrac{\dfrac{x_2}{x_1}-1}{\ln\dfrac{x_2}{x_1}},\end{split}$$ 令$\dfrac{x_2}{x_1}=t$，其中$t>1$，则 $$x_1+x_2=\dfrac{1-\dfrac 1t}{\ln t}+\dfrac{t-1}{\ln t}=\dfrac{t-\dfrac 1t}{\ln t},$$ 因此只需要证明 $$\forall t>1,t-\dfrac 1t-2\ln t>0.$$ 考虑到 $$\left(t-\dfrac 1t-2\ln t\right)'_t=\left(\dfrac 1t-1\right)^2>0,$$ 于是左边不等式得证．

对称构造

可以参考每日一题[83] 极值点偏移不等式的对称化构造，令$g(x)=\dfrac{1}{x}+\ln x$，证明

$$\forall t\in (0,1),g(1-t)>g(1+t)$$ 即可．事实上，有 $$g(1-t)-g(1+t)=\dfrac{2t}{1-t^2}+\ln\dfrac{1-t}{1+t},$$ 考虑到 $$\left(\dfrac{2t}{1-t^2}+\ln\dfrac{1-t}{1+t}\right)'_t=\dfrac{4t^2}{\left(1-t^2\right)^2}>0,$$ 于是左边不等式得证．

再证明右边的不等式．

齐次化

右边的不等式等价于

$$\ln\dfrac{x_1+x_2+1}{3}+1-a<0,$$ 将 $$\begin{split}&x_1+x_2=\dfrac{t^2-1}{t\ln t},\\&a=\dfrac {1}{x_1}+\ln x_1=\dfrac{t\ln t}{t-1}+\ln\dfrac{t-1}{t\ln t},\end{split}$$ 代入，该不等式左边为 $$\ln\dfrac{t^2-1+t\ln t}{t-1}-\dfrac{t\ln t}{t-1}+1-\ln 3,$$ 其导函数为 $$\dfrac{t\ln^2t-(t-1)^2}{\left(t^2-1+t\ln t\right)\left(t-1\right)^2}.$$ 因此只需要证明 $$\forall t>1,\sqrt t\ln t-t+1<0,$$ 即 $$\forall t>1,2\ln \sqrt t<\sqrt t-\dfrac{1}{\sqrt t},$$ 根据第(1)小问，于是右边不等式得证．

放缩法

令$x_0={\mathrm e}^{a-1}$，则$1+\ln x_0-a=0$，于是可知$x_0$是函数

$$h(x)=1+x\ln x -ax$$ 的极小值点．根据题意，有 $$x_1<x_0<x_2,$$ 于是 $$\dfrac{x_1}{x_0}<1<\dfrac{x_2}{x_0},$$ 应用我们熟知的不等式 $$\begin{split}\forall x\in (0,1),\ln x<\dfrac{2(x-1)}{x+1},\\\forall x>1,\ln x>\dfrac{2(x-1)}{x+1},\end{split}$$ 可得 $$\begin{split}\ln\dfrac{x_1}{x_0}&<\dfrac{2(x_1-x_0)}{x_1+x_0},\\\ln\dfrac{x_2}{x_0}&>\dfrac{2(x_2-x_0)}{x_2+x_0}.\end{split}$$ 又 $$\ln x_1=a-\dfrac{1}{x_1}=1+\ln x_0-\dfrac{1}{x_1},$$ 从而有 $$\ln\dfrac{x_1}{x_0}=1-\dfrac 1{x_1},$$ 同理有 $$\ln\dfrac{x_2}{x_0}=1-\dfrac 1{x_2},$$ 这样就有 $$\begin{split}1-\dfrac{1}{x_1}&<\dfrac{2(x_1-x_0)}{x_1+x_0},\\1-\dfrac{1}{x_2}&>\dfrac{2(x_2-x_0)}{x_2+x_0},\end{split}$$ 从而可得 $$-x_1^2-x_1+3x_1x_0<-x_2^2-x_2+3x_2x_0,$$ 即 $$3(x_2-x_1)x_0-(x_2-x_1)(x_2+x_1+1)>0,$$ 两边同除以$x_2-x_1$，即得 $$x_1+x_2<3x_0-1=3{\mathrm e}^{a-1}-1,$$ 于是右边不等式得证．

---

最后留两个练习题．

1、已知$f(x)=-a{\mathrm e}^{2x}+(2-a){\mathrm e}^x+x$，其中$a$为常数．方程$f(x)=0$的两个根为$x_1$、$x_2$，并且满足$x_1<x_2<\ln\dfrac 2a$，求证：$a\left({\mathrm e}^{x_1}+{\mathrm e}^{x_2}\right)>2$．

2、已知函数$f(x)=x-a{\rm e}^x$，其中$a\in\mathcal R$．已知函数$y=f(x)$有两个零点$x_1,x_2$且$x_1<x_2$．

（1）求证：$\dfrac{x_2}{x_1}$随着$a$的减小而增大；

（2）求证：$x_1+x_2$随着$a$的减小而增大．